Bandpass filter design calculations

What is a Bandpass Filter?

A bandpass filter is an electronic filter that allows signals within a certain frequency range (called the passband) to pass through while attenuating signals outside of this range. It combines the features of both low-pass filters (which allow low-frequency signals to pass) and high-pass filters (which allow high-frequency signals to pass). The filter is designed to allow only a specific range of frequencies to pass through and block frequencies below and above that range.

A bandpass filter has two main parameters:

1. Lower cutoff frequency (fL​ ): The frequency below which signals are attenuated.
2. Upper cutoff frequency (fH​ ): The frequency above which signals are attenuated.
3. The bandwidth (BW) of the filter is the difference between the upper and lower cutoff frequencies: BW=fH−fL​ .

Why Use a Bandpass Filter?

Bandpass filters are used in various applications where specific frequency ranges need to be isolated. Some reasons to use a bandpass filter include:

• Selective signal filtering: In applications where only a narrow band of frequencies is important (e.g., in communication systems, radio, and audio equipment), a bandpass filter ensures that only those frequencies pass through.
• Noise rejection: Bandpass filters can remove unwanted signals or noise that are outside the frequency range of interest.
• Signal separation: In systems where different signals occupy different frequency bands (e.g., in spectrum analysis or audio processing), bandpass filters are used to isolate each frequency band.

How Does a Bandpass Filter Work?

A bandpass filter works by combining the characteristics of a low-pass filter and a high-pass filter:

1. A high-pass filter allows frequencies above a certain cutoff (usually denoted as fL​ ) to pass while blocking lower frequencies.
2. A low-pass filter allows frequencies below a certain cutoff (usually denoted as fH​ ) to pass while blocking higher frequencies.

The bandpass filter allows frequencies between fL​ and fH​ to pass while blocking both frequencies below fL​ and above fH​ .

• Passband: The range of frequencies between the lower and upper cutoff frequencies.
• Stopband: Frequencies outside the passband that are attenuated.

Bandpass Filter Design Calculations

The design of a bandpass filter typically involves selecting the appropriate components (resistors, capacitors, and sometimes inductors) to achieve the desired center frequency f0​ , lower cutoff frequency fL​ , and upper cutoff frequency fH​ .

Center Frequency and Bandwidth:

The center frequency (f0​ ) of a bandpass filter is the frequency at which the filter's response is maximized. It is the average of the lower and upper cutoff frequencies:

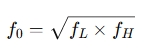
The bandwidth (BW) is the difference between the upper and lower cutoff frequencies:

BW = f H​ − f L​

Filter Types and Calculations:

• RLC Circuit (Resistor-Inductor-Capacitor): For a simple bandpass filter made with resistors, inductors, and capacitors (RLC circuit), the center frequency and bandwidth are related by:

  

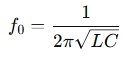
  Where:

  • f0​ is the center frequency (Hz)
  • L is the inductance (Henries)
  • C is the capacitance (Farads)

  The bandwidth of a standard RLC circuit is given by:

  

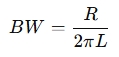
  Where:

  • R is the resistance (Ohms)

  These equations help you design the components (resistors, capacitors, and inductors) to achieve the desired center frequency and bandwidth for your application.

• Active Bandpass Filter (Op-Amp based): In an active bandpass filter using operational amplifiers (op-amps), you can use the following formulas to determine the cutoff frequencies and center frequency.

  For a second-order bandpass filter using op-amps, the center frequency and bandwidth are calculated similarly to the RLC circuit, but the design involves selecting appropriate resistor and capacitor values for the op-amp configuration.

  • Center frequency formula:
    
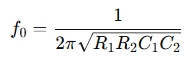
  • Bandwidth formula:
    

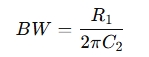
  Where R1​ , R2​ , C1​ , and C2​ are the resistors and capacitors in the op-amp circuit. These values are chosen based on the desired filter characteristics.

Q Factor (Quality Factor):

The Q factor describes the selectivity of the bandpass filter. It is the ratio of the center frequency to the bandwidth:

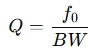
A high Q factor indicates a narrow passband and better selectivity, meaning the filter is more sensitive to frequencies around the center frequency. A low Q factor indicates a broader passband.

When Should You Use Bandpass Filter Design Calculations?

You should use bandpass filter design calculations when you need to:

1. Isolate a specific frequency band: When you need to pass a narrow band of frequencies and filter out unwanted frequencies, such as in communications (e.g., radio or cell phone transmission).
2. Remove noise: In situations where you want to remove high- or low-frequency noise from a signal and isolate the frequency of interest.
3. Audio systems: In audio processing, for example, to pass certain frequency ranges to specific speakers (e.g., passing mid-range frequencies to a mid-range speaker or bass frequencies to a subwoofer).
4. Signal processing: In applications like radar, instrumentation, and analysis where specific frequency ranges need to be captured and analyzed.

Practical Examples:

1. Radio Communication: Bandpass filters are used to allow only the radio frequency of interest to pass, while filtering out other frequencies.
2. Audio Systems: In audio systems, a bandpass filter can be used in crossovers to send only the frequencies that correspond to the speakers' capabilities (e.g., sending low frequencies to the subwoofer and high frequencies to the tweeters).
3. Instrumentation: In signal processing for instrumentation systems (such as measuring signals from sensors), bandpass filters isolate the desired frequency components for analysis.
4. Optical Systems: Bandpass filters are used in optical applications to isolate specific wavelengths of light, such as in fluorescence microscopy.

 

Bandpass filter design calculations