Speaker crossover calculation formula
Speaker Crossover Circuit Calculator
First order (6dB/octave) two-way crossover
Second order (12 dB/octave) two-way crossover |
A Speaker Crossover Calculation Formula is a mathematical tool or set of formulas used to design the crossover networks that divide an audio signal into different frequency ranges (like bass, midrange, and treble) for driving different types of speakers (such as woofers, midrange drivers, and tweeters) within a speaker system.
What is a Speaker Crossover?
A crossover is an electronic filter used in speaker systems to direct certain frequency ranges to specific drivers (e.g., sending low frequencies to a woofer and high frequencies to a tweeter). Crossovers are used to ensure that each driver in a multi-driver speaker system only handles the frequencies it's designed for, ensuring better sound quality and preventing damage to the speakers.
Why Use a Speaker Crossover Calculation Formula?
- Proper frequency distribution: To ensure that each speaker (woofer, midrange, or tweeter) only plays the frequencies it's designed for, which enhances overall sound quality and prevents distortion or speaker damage.
- System performance: To achieve a balanced sound across the frequency spectrum, ensuring that low, mid, and high frequencies are properly handled by the appropriate drivers.
- Speaker protection: Proper crossover design can help prevent a speaker from receiving signals (either too low or too high in frequency) that it can't reproduce well or could be damaged by.
- Design optimization: If you’re designing a custom speaker system, calculating crossovers helps you build a system that meets your performance requirements.
How Does a Speaker Crossover Calculation Formula Work?
The crossover frequency is determined based on the filter type (e.g., low-pass or high-pass) and the components (capacitors and inductors) in the crossover network. Here are the basic formulas for calculating crossover frequency for low-pass and high-pass filters:
Crossover Frequency Formula:
For a 2nd-order Butterworth filter, the most common type used in speaker crossovers:
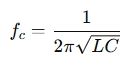
Where:
- fc = crossover frequency (in Hz)
- L = inductance (in Henries, H)
- C = capacitance (in Farads, F)
For a simple 1st-order crossover (often used in basic systems), you can use these formulas:
- For a low-pass filter (for the woofer):
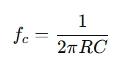
Where:
-
R = resistance (in ohms, Ω)
-
CC C = capacitance (in farads, F)
-
fc = crossover frequency (in Hz)
-
For a high-pass filter (for the tweeter):
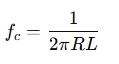
Where:
- L = inductance (in Henries, H)
How to Use These Formulas:
- Determine the crossover frequency you want (e.g., 3,000 Hz for a typical midrange-to-tweeter crossover).
- Select appropriate components (capacitors and inductors) based on the desired frequency. For example, for a low-pass filter, you’ll choose an inductor with the right value of inductance (LL L) to achieve the desired crossover frequency.
Example for a Low-Pass Filter:
If you want a crossover frequency of 2,000 Hz for a woofer, and you have a capacitor value of 10 μF, you can use the formula:
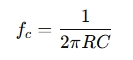
Rearrange to solve for R:
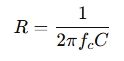
Substitute the values:
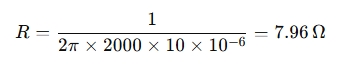
So, for a 2,000 Hz crossover with a 10 μF capacitor, you would need a resistor with a value of approximately 7.96 Ω.
When Should You Use a Speaker Crossover Calculation Formula?
- Designing custom speaker systems: When building your own speaker setup, you’ll need to calculate and design the crossovers to ensure that each driver only handles the frequencies it can reproduce best.
- Upgrading or repairing speakers: If you’re modifying or repairing an existing speaker system, calculating and replacing the crossovers may be necessary to improve performance.
- Tuning an audio system: If you're adjusting the frequency response of a multi-speaker setup (like in home audio systems or car audio systems), crossovers will be essential to match the system's needs.
Additional Considerations:
- Order of the filter: The most common filters are 1st and 2nd order filters, with 2nd order providing steeper slopes for frequency separation.
- Component tolerance: Components like capacitors and inductors can have a tolerance range, meaning the actual frequency may differ slightly from the calculated one, so you may need to adjust based on the actual performance.