Calculation of 3D vector angle

Vector V1: ,,
Vector V2: ,,
 
Angle：

What is the Calculation of a 3D Vector Angle?

The calculation of a 3D vector angle refers to finding the angle θ between two vectors in three-dimensional space. This angle represents how much one vector needs to rotate to align with the other.

Why Calculate the Angle Between 3D Vectors?

  • To measure the orientation difference between two directions.
  • To determine whether vectors are perpendicular (90°) or parallel (0° or 180°).
  • To analyze motion, forces, and rotations in physics and engineering.
  • In graphics and game development, for lighting, camera angles, and object alignment.

How to Calculate the Angle Between Two 3D Vectors?

Given two vectors:

A=(Ax,Ay,Az)
B=(Bx,By,Bz)

  1. Use the Dot Product Formula:
    The angle θ between the two vectors can be found using the dot product formula: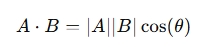

    where:

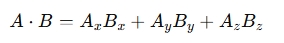
    is the dot product, and

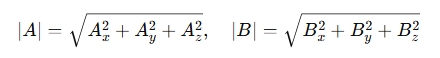
    are the magnitudes of the vectors.

  2. Solve for θ:

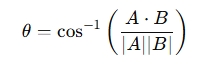
    where cos⁻¹ (arccos) gives the angle in radians.

  3. Convert to Degrees (if needed):

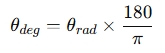
When to Use This Calculation?

  • Physics & Engineering: To determine forces and angles between moving objects.
  • Robotics: To calculate joint movements and orientations.
  • Computer Graphics: For shading, lighting, and animations.
  • Navigation & GPS: To compute directional differences between locations.