Bernoulli Inequality Calculator

Number X：
Power(n)：
Results:

What is a Bernoulli Inequality Calculator?

A Bernoulli Inequality Calculator is a tool that verifies or calculates values based on Bernoulli’s Inequality, which states:

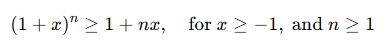
This inequality is useful in approximations, mathematical proofs, and financial calculations involving compound interest.

Why Use a Bernoulli Inequality Calculator?

  1. Verification of Inequality – Check if a given set of values satisfies Bernoulli’s Inequality.
  2. Quick Calculations – Avoids manual computation errors.
  3. Mathematical Proofs – Helps with proving inequalities and bounds in algebra and calculus.
  4. Finance & Growth Models – Used in compound interest and exponential growth approximations.

How Does a Bernoulli Inequality Calculator Work?

The calculator typically requires:

  • x (real number, x ≥ -1)
  • n (positive integer, n ≥ 1)

It computes:

  • (1+x)n
  • 1+nx
  • Compares them to verify if the inequality holds.

When to Use a Bernoulli Inequality Calculator?

  • Math & Science Problems – To verify inequalities in exams or research.
  • Finance & Economics – To approximate interest growth.
  • Algorithm Design – Used in probability theory and machine learning.