Three Points Collinear Calculator
What is a Three Points Collinear Calculator?
A Three Points Collinear Calculator is a tool that checks whether three given points lie on the same straight line. Three points (x1,y1), (x2,y2), and (x3,y3) are collinear if they lie on the same straight line.
Why Use a Three Points Collinear Calculator?
- Quick Verification – Instead of manually calculating, it instantly checks collinearity.
- Error-Free Computation – Avoids mistakes in manual calculations.
- Geometric Applications – Useful in coordinate geometry, physics, and computer graphics.
- Programming & GIS – Helps in map-based applications and spatial analysis.
How Does a Three Points Collinear Calculator Work?
It uses one of the following methods:
1. Slope Formula Method
Three points are collinear if the slope between any two pairs is the same:
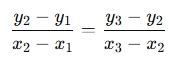
If the slopes are equal, the points are collinear.
2. Area of Triangle Method
If the area of the triangle formed by the three points is zero, they are collinear. The area is given by:
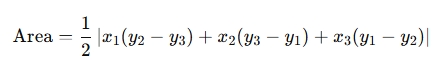
If the area = 0, the points are collinear.
When to Use a Three Points Collinear Calculator?
- Geometry & Trigonometry Problems – To check if points are on the same line.
- Physics & Engineering – Used in motion analysis and structural design.
- Programming & GIS Mapping – Important in spatial data analysis and game development.