Complex Number Calculator

Complex multiplication [ (a+bi) × (a+bi) ]
a: bi:
a: bi:
Multiplication：
Complex number division [ (a+bi) / (a+bi) ]
a: bi:
a: bi:
Division：
Complex square root： [ r1 = x+yi ; r2 = -x-yi ]
a: bi:
r1 :
r2 :

A Complex Number Calculator is a tool used to perform mathematical operations with complex numbers. Complex numbers consist of two parts: a real part and an imaginary part, and they are written in the form a + bi, where:

  • a is the real part
  • b is the imaginary part
  • i is the imaginary unit, defined as i2=−1

Why Use a Complex Number Calculator?

  1. Mathematical Operations: Complex numbers are used in various fields such as engineering, physics, and applied mathematics. They are essential in solving problems related to electrical circuits, waveforms, and many other phenomena.

  2. Ease of Use: A calculator simplifies operations with complex numbers, such as addition, subtraction, multiplication, division, and finding magnitudes or angles.

  3. Visual Representation: Complex numbers are often represented on the complex plane. The calculator can help you visualize these numbers in both rectangular and polar forms.

How Does It Work?

A Complex Number Calculator typically lets you input complex numbers and perform operations like:

  1. Addition/Subtraction: Adding or subtracting the real and imaginary parts separately.

    • Example: (3+4i)+(1+2i)=(3+1)+(4i+2i)=4+6i

  2. Multiplication: Distribute the terms and use the property that i2=−1.

    • Example: (3+2i)×(1+4i)=3(1+4i)+2i(1+4i)=3+12i+2i+8i2=3+14i−8=−5+14i

  3. Division: Multiply by the conjugate of the denominator to simplify.

    • Example: 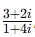, multiply both the numerator and denominator by the conjugate of the denominator (1 - 4i).

  4. Magnitude: Calculate the magnitude (or absolute value) of a complex number, defined as

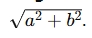
  5. Polar Form: Express complex numbers in polar coordinates, often using the formula r(cos⁡θ+isin⁡θ), where rr r is the magnitude and θ\theta θ is the angle.

When to Use It?

  • When dealing with complex numbers in mathematics, physics, engineering, and related fields.
  • When solving equations involving complex roots, like quadratic equations with negative discriminants.
  • When visualizing the behavior of complex numbers in different forms, such as rectangular or polar.