Calculate the distance from point to line

Line： X +  Y = 
Point：  , 
Distance

What is Distance from a Point to a Line?

The distance from a point to a line is the shortest (perpendicular) distance between a given point and a straight line in a 2D or 3D space.

Formula for 2D (Ax + By + C = 0)

If the line equation is given in standard form as:

Ax+By+C=0

And the point is (x0,y0), the perpendicular distance dd d is calculated as:

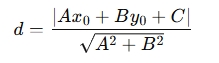
Formula for 3D

For a line defined parametrically by:

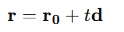
And a point P, the distance is given by:

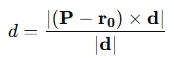
Where:

  • r0​ is a point on the line,
  • d is the direction vector,
  • × represents the cross product.

Why Calculate the Distance?

  • Geometry & Trigonometry: Used in coordinate geometry for shortest path calculations.
  • Physics & Engineering: Important for measuring shortest distances in structures and mechanics.
  • Computer Graphics: Used in collision detection and rendering.
  • Machine Learning: Applied in clustering algorithms (e.g., K-means).
  • Navigation & GPS: Used in mapping and route optimization.

How to Calculate It?

  1. Identify the given data: The equation of the line and coordinates of the point.
  2. Plug values into the formula.
  3. Compute the absolute numerator.
  4. Compute the denominator (square root part).
  5. Divide and get the shortest distance.

When to Use It?

  • In geometry: Finding the shortest distance between a landmark and a road.
  • In engineering: Determining the minimum clearance between objects.
  • In robotics & AI: For obstacle avoidance.
  • In physics: Calculating shortest travel paths.