Exponential Function Solver Calculator
An Exponential Function Solver Calculator is a tool used to solve exponential equations or functions.
What is an Exponential Function?
An exponential function is a mathematical function of the form:
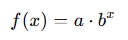
Where:
- a is a constant (often the initial value or coefficient),
- b is the base (a constant greater than 0 and not equal to 1),
- x is the exponent (which can be any real number).
In exponential functions, the variable x is the exponent, which means the function grows (or decays) very quickly as x increases or decreases.
Example:

Why Use an Exponential Function Solver Calculator?
An Exponential Function Solver Calculator is useful for:
- Solving exponential equations: Sometimes you need to find the value of xx x that satisfies an equation like a⋅bx=c.
- Graphing exponential functions: If you want to understand how an exponential function behaves visually, a calculator can plot the curve.
- Simplifying complex calculations: Exponential functions often involve large numbers, so a calculator helps to quickly and accurately find results without manually calculating large powers.
How Does It Work?
To solve an exponential function equation, you usually want to find the value of x that makes the equation true.
For example, if you have the equation:
3⋅2x=24Here’s how the calculator works to solve it:
-
Isolate the exponential part: Divide both sides by 3:
2x=8 -
Rewrite the equation in terms of the same base: 8 can be written as 23, so:
2x=23 -
Solve for x: Since the bases are the same, we can set the exponents equal to each other:
x=3
In this case, the solution to the equation is x=3.
A solver calculator does all these steps automatically. You simply input the exponential equation, and the calculator will solve for x (or any other variable).
When Should You Use It?
You would use an exponential function solver calculator in situations like:
- In Algebra: When solving equations with exponential terms (e.g., 5⋅3x=45).
- In Growth or Decay Problems: Exponential functions are often used to model things that grow or decay at a constant rate, like population growth, radioactive decay, or compound interest.
- In Logarithms: Since logarithms are the inverse of exponentiation, you can use a calculator to solve exponential equations using logarithms, such as solving for x in equations like 2x=100 using the natural logarithm.
- In Finance: Exponential functions can model compound interest, investment growth, or savings account growth over time.
- In Science/Physics: Exponential functions describe things like radioactive decay, certain biological processes, and the intensity of light or sound over distance.