Fibonacci Number Calculator

Enter calculated value
Fibonacci sequence number：=
Fibonacci Sequence：=

A Fibonacci Number Calculator is a tool that computes the Fibonacci sequence for a given number. The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding ones, typically starting with 0 and 1. The sequence looks like this:

0,1,1,2,3,5,8,13,21,34,55,…

Mathematically, the nn n-th Fibonacci number is defined as:

F(n)=F(n−1)+F(n−2)

with initial conditions:

F(0)=0,F(1)=1

Why Fibonacci Calculations are Important:

The Fibonacci sequence is significant in various fields such as:

  • Mathematics: The Fibonacci sequence appears in number theory, combinatorics, and geometry.
  • Nature and Biology: Fibonacci numbers are found in the arrangement of leaves, flowers, and fruits (e.g., the branching of trees or the petals of flowers).
  • Computer Science: Fibonacci numbers are used in algorithms, particularly for dynamic programming problems, recursive algorithms, and in the construction of efficient data structures like Fibonacci heaps.
  • Finance: Some traders use Fibonacci numbers to make predictions and analyze price movements in the stock market (Fibonacci retracements).

How to Calculate Fibonacci Numbers:

The Fibonacci sequence can be computed by using different methods:

  1. Recursion: Each number is the sum of the two preceding numbers. This is simple but inefficient for large nn n due to redundant calculations.
    F(n)=F(n−1)+F(n−2)
  2. Iteration: This method uses loops to calculate Fibonacci numbers more efficiently.
  3. Formula (Closed Form): There's a mathematical formula called Binet’s Formula that directly computes the Fibonacci number without needing to iterate:

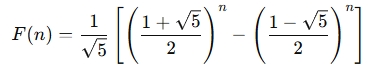
    This formula is more complex but can be used for an exact result.

When to Use a Fibonacci Number Calculator:

A Fibonacci Number Calculator is useful when:

  • You need to calculate a specific Fibonacci number efficiently, especially for large numbers.
  • You are studying or solving problems related to the Fibonacci sequence in mathematics, computer science, or finance.
  • You are analyzing natural patterns and phenomena that follow the Fibonacci sequence.
  • You need to implement algorithms that require Fibonacci numbers, such as dynamic programming problems or certain sorting techniques.