Simplest quadratic root calculator

Enter number：
Results:
The simplest quadratic root：
X√

A simplest quadratic root calculator is a tool or method used to find the solutions (or roots) of a quadratic equation. A quadratic equation has the form:

ax2+bx+c=0

where:

  • a, b, and c are constants (with a≠0),
  • x is the variable we're solving for.

Why use a quadratic root calculator?

It simplifies the process of finding the roots of a quadratic equation, especially if the quadratic doesn't factor easily. Instead of manually applying the quadratic formula or factoring, the calculator gives you the solutions quickly and accurately.

How does it work?

The quadratic formula is used to calculate the roots of the equation. The formula is:

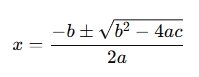
Where:

  • b2−4ac is called the discriminant. It determines the nature of the roots:
    • If b2−4ac>0, there are two real and distinct roots.
    • If b2−4ac=0, there is one real repeated root.
    • If b2−4ac<0, there are no real roots (but two complex roots).

When to use it?

  • When you encounter a quadratic equation in algebra, physics, engineering, or any field that involves mathematical modeling.
  • It is particularly helpful when factoring the quadratic is difficult or impossible.

You can use the simplest quadratic root calculator by simply inputting the values for a, b, and c, and it will output the roots based on the formula.