Consecutive natural number cubes and calculator
What Are Consecutive Natural Number Cubes?
Consecutive natural number cubes refer to the cubes of consecutive natural numbers. A natural number is a positive integer (1, 2, 3, 4, 5, ...), and the cube of a number is that number multiplied by itself twice (n³ = n × n × n).
For example:
- The cube of 1 is 13=1
- The cube of 2 is 23=8
- The cube of 3 is 33=27
- The cube of 4 is 43=64
- And so on.
These are considered "consecutive" because they follow each other in the sequence of natural numbers.
Why Do We Use Consecutive Natural Number Cubes?
Consecutive natural number cubes are important in various areas of mathematics, particularly in algebra, number theory, and sometimes in geometric applications. These cubes have interesting properties, such as forming sums or patterns when analyzed in groups.
For example:
- The sum of the first few cubes of consecutive natural numbers has a known formula:
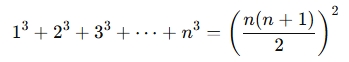
This is the square of the sum of the first n natural numbers.
How Are Consecutive Natural Number Cubes Used?
-
Mathematical Proofs and Problems: Consecutive natural number cubes are often used in solving problems related to sequences, series, and summations.
-
Geometric Interpretation: In some cases, cubes can be related to 3-dimensional objects, such as cubes or blocks in a grid, helping us visualize volume or spatial relations.
-
Calculations: You might need a calculator to quickly compute the cubes of larger numbers. For instance, if you're working with large values or need to sum multiple cubes, a calculator can help avoid manual errors.
When Do We Use Calculators for Natural Number Cubes?
We typically use calculators when dealing with larger numbers where calculating cubes by hand becomes tedious. For example:
- If you need to calculate the cube of 50 (which is 503=125,000),
- If you are working with a sequence of large numbers and need to calculate their cubes and possibly sum them up.
Most scientific calculators or calculators on your phone or computer can quickly calculate cubes by using a cube function or simply multiplying the number by itself twice.