Parabola Vertex Calculator

Y = X2 +  X + 
Vertex X-axis coordinate：
Vertex Y-axis coordinate：

A Parabola Vertex Calculator is a tool that helps you find the vertex of a parabola given its equation or certain parameters. The vertex of a parabola is the highest or lowest point on the curve, depending on whether the parabola opens upwards or downwards. It represents the point where the parabola changes direction, and it plays a crucial role in graphing quadratic equations and analyzing their properties.

What is a Parabola Vertex?

A parabola is a U-shaped curve that is the graph of a quadratic function. The vertex is the point where the parabola reaches its maximum or minimum value. For a quadratic equation of the form:

y=ax2+bx+c

  • The vertex occurs at the x-coordinate given by the formula:

    x = −b / 2ax

  • Once you know the x-coordinate of the vertex, you can substitute it into the original equation to find the y-coordinate of the vertex.

What is a Parabola Vertex Calculator?

A Parabola Vertex Calculator is a tool that calculates the vertex (both the x and y coordinates) of a parabola, given the coefficients of the quadratic equation ax2+bx+c. The calculator uses the formula for the x-coordinate of the vertex and then substitutes it back into the equation to find the corresponding y-coordinate.

Why Use a Parabola Vertex Calculator?

  1. Time-Saving: Calculating the vertex manually can take time, especially when working with complex quadratic equations. A vertex calculator provides quick results.
  2. Accuracy: The calculator ensures that you get the correct coordinates for the vertex, reducing the chance of human error in your calculations.
  3. Graphing: The vertex is essential for graphing a parabola accurately. Knowing the vertex helps you understand the shape and position of the parabola on a graph.
  4. Analyzing Quadratic Functions: The vertex provides valuable information about the behavior of the function, such as the minimum or maximum value. This is especially useful in optimization problems or in physics, economics, and engineering.

How Does a Parabola Vertex Calculator Work?

  1. Input: You input the coefficients aa a, bb b, and cc c from the quadratic equation y=ax2+bx+c.

  2. Calculate the x-coordinate: The calculator calculates the x-coordinate of the vertex using the formula:

    x=−b / 2a

  3. Calculate the y-coordinate: The calculator substitutes the x-coordinate into the original equation y=ax2+bx+c to calculate the y-coordinate of the vertex.

  4. Output: The calculator provides the vertex coordinates (x,y), representing the highest or lowest point of the parabola.

Example:

Let’s say you have the quadratic equation:

y=2x2−8x+3
  • The x-coordinate of the vertex is calculated using the formula x=−b / 2a ​ :
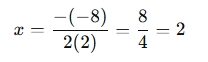
  • Then, to find the y-coordinate, you substitute x=2 into the equation y=2x2−8x+3:
y=2(2)2−8(2)+3=2(4)−16+3=8−16+3=−5

So, the vertex of the parabola is (2,−5).

When to Use a Parabola Vertex Calculator?

  1. Graphing Quadratic Functions: If you're graphing a parabola, the vertex is a key point to plot. The vertex calculator gives you this information easily.

  2. Analyzing Quadratic Functions: The vertex tells you if the parabola has a minimum or maximum value. It’s helpful when you're solving optimization problems in calculus, physics, or economics.

  3. Solving Optimization Problems: In problems where you need to maximize or minimize a quadratic function (e.g., finding the maximum profit in a business problem or the maximum height of a projectile), the vertex gives you the solution directly.

  4. Physics and Engineering: In physics, the motion of objects in projectile motion, for example, follows a parabolic path. The vertex provides the maximum height. Similarly, in engineering, optimization often involves finding the vertex of a parabola.

  5. Calculus: The vertex is also used in calculus, especially in finding the turning points of a quadratic function, which are key for understanding the behavior of the function.