Line Intercept Calculator
A Line Intercept Calculator is a tool that helps you find the points where a line intersects the coordinate axes (the x-intercept and y-intercept) given the equation of a line. These intercepts are critical points that help define the position of the line on a graph and are used in solving many geometric and algebraic problems.
What is a Line Intercept?
- The x-intercept is the point where the line crosses the x-axis. At this point, the value of y is zero.
- The y-intercept is the point where the line crosses the y-axis. At this point, the value of x is zero.
The general equation of a line is typically written as:
y=mx+bwhere:
- mm m is the slope of the line,
- b is the y-intercept (the point where the line crosses the y-axis).
What is a Line Intercept Calculator?
A Line Intercept Calculator is a tool that helps you find the x-intercept and y-intercept of a line based on its equation. You input the equation of the line into the calculator, and it computes the points where the line intersects the x-axis and y-axis.
Why Use a Line Intercept Calculator?
- Efficiency: Finding the intercepts manually can involve solving equations. The calculator simplifies this process by quickly providing the intercepts.
- Accuracy: The calculator ensures that the intercepts are calculated correctly, saving time and reducing the risk of errors in manual calculations.
- Graphing: The intercepts are crucial for graphing linear equations. Knowing where the line crosses the axes helps you plot the line accurately on a graph.
- Problem Solving: In many algebraic and real-world problems, you need to find the intercepts to solve for unknowns or understand the relationship between variables.
How Does a Line Intercept Calculator Work?
A Line Intercept Calculator works by taking the equation of a line and applying the following steps to find the intercepts:
-
Input: You enter the equation of the line, typically in the form y=mx+b, where mm m is the slope and b is the y-intercept.
-
Calculate the y-intercept: The y-intercept is the value of b in the equation y=mx+b. This is the point where the line crosses the y-axis, and it is directly given by the value of b.
-
Calculate the x-intercept: To find the x-intercept, you set y=0 in the equation and solve for x. The equation becomes:
0=mx+bSolving for x gives:
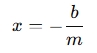
This is the x-coordinate of the point where the line crosses the x-axis.
-
Output: The calculator provides the x-intercept and y-intercept as the result.
Example:
Let’s say you have the equation of a line:
y=2x+6- The y-intercept is simply the value of b, which is 6. This means the line crosses the y-axis at (0,6).
- To find the x-intercept, you set y=0 and solve for x:
0=2x+6
2x=−6
x=−3
So, the line crosses the x-axis at (−3,0).
When to Use a Line Intercept Calculator?
-
Graphing: When you are graphing a linear equation, knowing the intercepts helps you plot the line accurately.
-
Solving Algebraic Problems: In many algebraic problems, such as finding the intersection of lines or solving systems of linear equations, you often need to find the intercepts.
-
Analyzing Relationships: The intercepts can help you understand the relationship between two variables in real-world problems. For instance, in economics or physics, you may need to interpret the intercepts as starting points or critical values.
-
Physics: In physics, linear models often describe relationships between variables. Finding the intercepts can give you important physical quantities, such as initial velocities or positions.
-
Optimization Problems: Sometimes, intercepts are used in optimization problems where you need to find the starting values of variables or where a condition is met (e.g., the point where a quantity is zero).
Summary:
A Line Intercept Calculator is a tool that helps you quickly find the points where a line intersects the x-axis and y-axis, which are the x-intercept and y-intercept. These intercepts are essential for graphing linear equations, solving algebraic problems, and analyzing real-world relationships in areas like physics, economics, and engineering.