Intersection point of two lines calculator
An Intersection Point of Two Lines Calculator is a tool used to determine the point where two lines intersect, given their equations. The intersection point is the point where both lines meet or cross each other on a graph. This point represents the values of x and y that satisfy both line equations simultaneously.
What is the Intersection Point of Two Lines?
The intersection point is the point where two lines meet. In mathematical terms, it’s the solution to the system of two equations:
Line 1: y1=m1x+b1Line 2: y2=m2x+b2
Where:
- m1 and m2 are the slopes of the lines,
- b1 and b2 are the y-intercepts.
The intersection point is the pair (x,y) that satisfies both equations. If the lines are not parallel, they will intersect at exactly one point. If the lines are parallel, they will either never intersect or coincide (in the case of identical lines).
Why Use an Intersection Point of Two Lines Calculator?
- Efficiency: Finding the intersection manually can be time-consuming, especially when dealing with complicated equations. A calculator can provide quick and accurate results.
- Accuracy: The calculator ensures that you get the correct values of x and y for the intersection point, reducing the risk of mistakes in manual calculations.
- Graphing: The intersection point is crucial for graphing two lines and understanding their relationship. Knowing where they meet helps visualize how the two lines interact on a graph.
- Solving Systems of Equations: The intersection point is the solution to a system of two linear equations. This method is useful in solving various real-world problems in physics, economics, and engineering, where you need to find the point at which two conditions are met.
How Does the Intersection Point of Two Lines Calculator Work?
The calculator works by following these steps:
-
Input: You input the equations of the two lines in the slope-intercept form (y=mx+b) or another linear equation form.
-
Set up the system of equations: The calculator sets up the system of equations representing the two lines:
- y=m1x+b1
- y=m2x+b2
-
Solve for x: The calculator solves the system of equations by setting the two y-values equal to each other (because at the intersection point, both lines have the same y-coordinate):
m1x+b1=m2x+b2Rearranging this equation to solve for x:
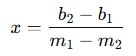
-
Substitute x into either equation: Once the value of x is found, substitute it back into either of the original line equations to solve for y:
y=m1x+b1 -
Output: The calculator provides the coordinates (x,y) of the intersection point.