Parabola Graph Calculator

A function is a correspondence in mathematics, which is the correspondence from a non-empty number set A to a real number set B. Simply put, if A changes with B, then A is a function of B. To be precise, let X be a non-empty set, Y be a non-empty number set, and f be a correspondence rule. If for each x in X, according to the correspondence rule f, there is a unique element y in Y corresponding to it, then the correspondence rule f is called a function on X, denoted as y=f(x), X is called the domain of the function f(x), the set {y|y=f(x), x∈R} is its range (the range is a subset of Y), x is called the independent variable, y is called the dependent variable, and it is customary to say that y is a function of x. The correspondence rule and the domain are two elements of a function.

You can move the graph up-down, left-right if you hold down the "Shift" key and then drag the graph.

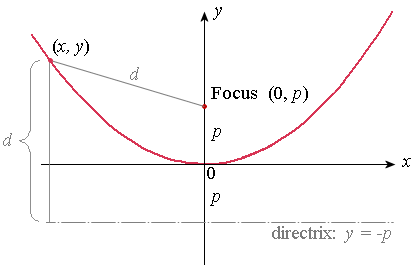
The parabola is defined as the locus of a point which moves so that it is always the same distance from a fixed point (called the focus) and a given line (called the directrix).

The focus of the parabola is at (0,p).

The directrix is the line y=−p.

The focal distance is |p| (Distance from the origin to the focus, and from the origin to the directrix. We take absolute value because distance is positive.)

The point (x, y) represents any point on the curve.

The distance d from any point (x, y) to the focus (0,p) is the same as the distance from (x, y) to the directrix.