Linear Interpolation Calculator
| First point coordinates | X1: | Y1: | ||
| The second point coordinates | X2: | Y2: |
| Target point x coordinate X : | |
| Y coordinate of target point | |
What is a Linear Interpolation Calculator?
A Linear Interpolation Calculator estimates unknown values between two known points on a straight line. It uses the linear interpolation formula to approximate a missing value.
Why Use a Linear Interpolation Calculator?
- Quick and Accurate Estimation – Saves time and reduces manual errors.
- Useful in Data Analysis – Helps estimate missing data points.
- Engineering & Science Applications – Used in physics, thermodynamics, and signal processing.
- Financial & Economic Analysis – Forecasting trends using existing data.
How Does a Linear Interpolation Calculator Work?
- Input Two Known Points – Given (x1,y1) and (x2,y2).
- Enter the Target x-Value – The x-value at which you need to find y.
- Apply the Linear Interpolation Formula:
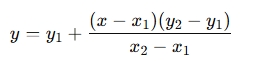
- Compute and Display the Result – The calculator provides the estimated y-value.
When is a Linear Interpolation Calculator Used?
- In mathematics & statistics – Estimating missing data points.
- In engineering & physics – Approximating values in experiments.
- In finance & economics – Predicting trends and market values.
- In computer graphics & gaming – Interpolating animations and shading effects.