Midpoint coordinate calculator between two points in three-dimensional space
A Midpoint Coordinate Calculator for three-dimensional space is a tool used to calculate the exact central point between two points in a 3D coordinate system. This central point is called the midpoint and is calculated by averaging the x, y, and z coordinates of the two given points.
Why Use a Midpoint Coordinate Calculator in 3D Space?
- Geometric Applications: Finding the central point of a line segment in 3D geometry.
- Navigation and Mapping: In 3D mapping systems (e.g., GPS, GIS), finding a midpoint between two points (e.g., locations or landmarks) can help in planning routes or understanding relationships in three-dimensional space.
- Physics and Engineering: In modeling physical systems (like movement of objects in space, positioning, or construction), finding the midpoint helps in calculations related to distance, balance, or force application.
- Graphics and 3D Modeling: Midpoint calculation is key for centering objects in 3D designs, animations, or game development.
How Does It Work?
The midpoint between two points in three-dimensional space, A(x1,y1,z1) and B(x2,y2,z2) , is calculated by averaging their corresponding x, y, and z coordinates:
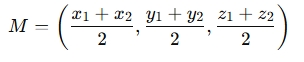
Where:
- M(x,y,z)is the midpoint.
- (x1,y1,z1) are the coordinates of point A.
- (x2,y2,z2) are the coordinates of point B.
This formula simply averages each of the three coordinates (x, y, z) to find the central point between the two.
When to Use a Midpoint Coordinate Calculator in 3D?
- In 3D geometry: When you need to find the midpoint of a line segment between two points.
- In 3D space navigation: To find the central location between two geographical points or objects.
- In engineering and design: For balancing or finding the average location of points in structural designs, robotics, or mechanical systems.
- In 3D graphics and animation: When placing objects or animations in the center between two points.
Using this calculator is especially useful in scenarios that involve 3D coordinate systems, such as computer graphics, physics simulations, engineering, or any application that involves positioning objects in a 3D environment.