Calculator for distance between two points in three-dimensional space and coordinates of midpoint

X Y Z
A :
B :
Distance between point A and point B
Coordinate midpoint：
x:y:z:

What is the Calculator for Distance Between Two Points in Three-Dimensional Space and Coordinates of Midpoint?

The distance between two points in three-dimensional space and the coordinates of the midpoint are two fundamental concepts in geometry. Given two points, the distance calculator provides the length of the straight line connecting them, while the midpoint calculator gives the average of their coordinates, representing the "middle point" between them.

1. Distance Between Two Points in 3D:

In three-dimensional space, the distance dd d between two points P1(x1,y1,z1) and P2(x2,y2,z2) is given by the distance formula:

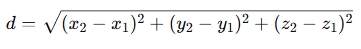
Where:

  • (x1,y1,z1) are the coordinates of the first point.
  • (x2,y2,z2) are the coordinates of the second point.

2. Midpoint Between Two Points in 3D:

The midpoint M between two points P1(x1,y1,z1) and P2(x2,y2,z2) is the point that lies exactly halfway between them. The coordinates of the midpoint are given by the midpoint formula:

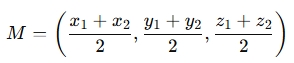
Why Use a Calculator for These Calculations?

  1. For Convenience and Accuracy: Calculating distance and midpoints manually can be time-consuming and prone to errors, especially when dealing with more complex points. A calculator automates the process and ensures precision.
  2. For Application in Real-World Problems: These calculations are important in physics, engineering, and computer graphics where precise spatial relationships between points need to be established, like in navigation, 3D modeling, or robotics.
  3. For Quick Comparison: A calculator can help quickly compare the relative distances and midpoints between multiple points, which is useful in data analysis, gaming, and other applications.

How Does It Work?

The calculations involve two main formulas:

  • Distance Formula: For any two points in three-dimensional space, you apply the distance formula to compute how far apart they are.
  • Midpoint Formula: To find the midpoint, you calculate the average of the coordinates in each dimension (x, y, and z).

You can either calculate these manually or use a calculator to input the coordinates, which will automatically compute the results for you.

When to Use a Calculator for Distance and Midpoint?

  • When you need precise measurements in 3D space: For example, in 3D modeling, computer simulations, or physics problems involving vector spaces.
  • In geometry or vector analysis problems: Calculating distances between points in space or finding the midpoint is common in geometric problems and vector analysis.
  • In navigation and mapping: For example, finding distances between GPS coordinates in 3D space or determining the central point between two locations.