Shortest distance calculator from point to plane
| Input Point: | , | , |
| Plane equation: | x+ | y+ | z+ | =0 |
| Shortest distance from point to plane: |
A Shortest Distance from Point to Plane Calculator is a tool used to calculate the perpendicular distance between a given point and a plane in 3D space. This is the shortest distance from the point to the plane, measured along a line that is perpendicular to the surface of the plane.
Why Use a Shortest Distance from Point to Plane Calculator?
This calculator is used to quickly find the shortest distance between a point and a plane, which is useful in geometry, physics, and engineering. It simplifies calculations and is important for problems involving projections, geometric analysis, or determining the minimum distance between a point and a surface.
How Does the Shortest Distance from Point to Plane Calculator Work?
The formula used to calculate the shortest distance dd d from a point P(x1,y1,z1) to a plane Ax+By+Cz+D=0 is:
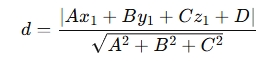
Where:
- (x1,y1,z1) are the coordinates of the point.
- A,B,C are the coefficients of the plane equation.
- D is the constant term in the plane equation.
Steps Involved:
- Input the coordinates of the point (x1,y1,z1) .
- Input the coefficients A,B,C,D from the equation of the plane Ax+By+Cz+D=0 .
- Apply the formula to calculate the perpendicular (shortest) distance from the point to the plane.
When to Use a Shortest Distance from Point to Plane Calculator?
You would use this calculator in the following scenarios:
- Geometric analysis: When determining how far a point is from a given plane in 3D space.
- Physics: In problems that involve projections, reflections, or interactions between a point and a plane.
- Engineering and computer graphics: When analyzing the distance between a point and a surface, such as in structural designs or modeling.