Slope of a Line Calculator
A Slope of a Line Calculator is a tool that helps you find the slope of a straight line when you know the coordinates of two points that lie on that line. The slope is a key geometric property that indicates how steep the line is. The calculator is designed to make this calculation faster and easier, especially when dealing with multiple lines or more complex problems.
What is the Slope of a Line?
The slope of a line, often denoted by mm m, is a measure of how much the y-coordinate of a point on the line changes relative to the x-coordinate as you move along the line. It describes the steepness and direction of the line.
Mathematically, the slope between two points (x1,y1) and (x2,y2) is calculated as:
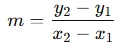
Where:
- m is the slope of the line.
- (x1,y1) and (x2,y2) are the coordinates of two points on the line.
- y2−y1 represents the change in y (vertical change).
- x2−x1 represents the change in x (horizontal change).
Why Use a Slope of a Line Calculator?
- Quick Calculation: It simplifies the process of calculating the slope when you're given two points, saving time, especially in larger datasets.
- Check Steepness: The slope tells you how steep the line is. A larger absolute value of the slope means a steeper line.
- Direction: The sign of the slope tells you the direction of the line. A positive slope means the line rises as it moves to the right, while a negative slope means the line falls as it moves to the right.
- Geometrical Analysis: It's useful for analyzing lines in coordinate geometry, physics, economics, and any field that uses linear relationships.
How Does the Slope of a Line Calculator Work?
- Enter Two Points: You provide the coordinates of two points on the line. These are typically given as (x1,y1) and (x2,y2).
- Apply the Formula: The calculator uses the formula:
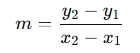
- Display the Result: It computes the slope and displays the result, which could be a positive, negative, or zero value.
- If the slope is positive, the line goes up as you move from left to right.
- If the slope is negative, the line goes down.
- A slope of zero means the line is horizontal, and an undefined slope means the line is vertical.
When to Use a Slope of a Line Calculator?
You would use a Slope of a Line Calculator when:
- You need to find the slope of a line between two known points.
- You’re working on geometry or algebra problems that require slope calculations, such as finding parallel or perpendicular lines (where slopes are equal or negative reciprocals).
- You’re analyzing trends or relationships between two variables in fields like economics, physics, or statistics.