3x3 third-order matrix determinant calculator

a = b= c =
d = e= f =
g = h= i =
Matrix determinant (|A|)=

What is a 3×3 Third-Order Matrix Determinant Calculator?

A 3×3 Third-Order Matrix Determinant Calculator is a tool that computes the determinant of a 3×3 matrix. The determinant is a scalar value that helps determine properties of the matrix, such as invertibility, linear dependence, and geometric transformations.

For a 3×3 matrix:

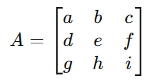
The determinant, det(A), is calculated using:

det⁡(A)=a(ei−fh)−b(di−fg)+c(dh−eg)

or using cofactor expansion along the first row:

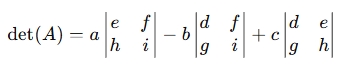
where each 2×2 determinant is computed as:

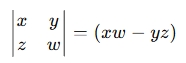
Why Use a 3×3 Determinant Calculator?

  1. Determines Invertibility – If det⁡(A)≠0 , the matrix has an inverse; otherwise, it does not.
  2. Used in Linear Algebra – Important for solving systems of equations.
  3. Geometric Interpretation – Represents volume scaling in transformations.
  4. Essential in Many Fields:
    • Physics & Engineering – In analyzing forces, stability, and systems.
    • Computer Graphics – Used in 3D transformations and projections.
    • Machine Learning & AI – Used in data transformations and feature analysis.
    • Cryptography & Security – Plays a role in encoding and transformations.

How Does It Work?

  1. Input a 3×3 matrix.

  2. Compute the determinant using the formula:

    det⁡(A)=a(ei−fh)−b(di−fg)+c(dh−eg)

    Display the determinant value.

Example Calculation

Given the matrix:

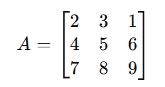
The determinant is:

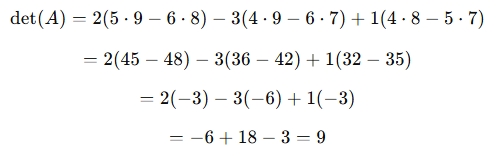
When to Use It?

  • In solving systems of equations – Used in Cramer's Rule.
  • In physics and engineering – For calculating torque, moment of inertia, and stability.
  • In computer graphics – For 3D transformations and projections.
  • In economics and data science – For statistical modeling and risk analysis.