Rank calculator for 4*4 third-order matrix
|
| |||||||||||||||||
|
| |||||||||||||||||
| Results: | |||||||||||||||||
| A + B = |
| ||||||||||||||||
| A - B = |
| ||||||||||||||||
What is a Rank Calculator for a 4×4 Matrix?
A Rank Calculator for a 4×4 Matrix determines the rank of a given 4×4 matrix. The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix.
For a 4×4 matrix:
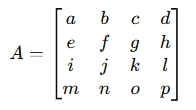
The rank of A is found by reducing the matrix to its row echelon form (REF) or reduced row echelon form (RREF) using Gaussian elimination or determinant-based methods.
Why Use a 4×4 Matrix Rank Calculator?
- Determines Linear Dependence – Helps analyze if rows or columns are dependent.
- Checks Solvability of Equations – A rank smaller than 4 indicates dependent equations.
- Used in Many Fields:
- Linear Algebra – Determines if a system of equations has a unique solution.
- Engineering & Physics – Stability analysis and signal processing.
- Machine Learning & Data Science – Feature selection and dimensionality reduction.
- Computer Graphics – Used in transformations and 3D modeling.
How Does It Work?
- Input a 4×4 matrix.
- Perform row operations to transform the matrix into row echelon form (REF) or reduced row echelon form (RREF).
- Count the number of nonzero rows, which gives the rank.
Example Calculation
Given the matrix:
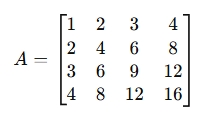
- Convert to Row Echelon Form (REF):

- The number of nonzero rows is 1, so rank(A) = 1.
When to Use It?
- To check system solvability – If rank < 4, the system may have infinite or no solutions.
- In physics & engineering – To analyze force and energy distribution.
- In machine learning – To determine feature independence in datasets.