Cramer's Law Determinant Calculator
| Results: | |||||||
| Δ = | ΔX = | ΔY = | ΔZ = | ||||
| X = | Y = | Z = | |||||
What is a Cramer’s Rule Determinant Calculator?
A Cramer’s Rule Determinant Calculator is a tool used to solve systems of linear equations using Cramer’s Rule, which relies on determinants. This method provides an explicit formula for the solution of a system of N equations with N unknowns, given that the coefficient matrix has a nonzero determinant.
Why is Cramer’s Rule Important?
Cramer’s Rule is useful for:
- Solving Small Linear Systems (2×2, 3×3, etc.)
- Directly finds the solution without row reduction or matrix inversion.
- Checking System Consistency
- If det(A) = 0, the system has no unique solution (either dependent or inconsistent).
- Understanding Determinants' Role in Linear Algebra
- Highlights the connection between determinants and solutions.
- Theoretical Applications in Physics & Engineering
- Used in electrical circuits, statics, and structural analysis.
How Does Cramer’s Rule Work?
Consider a system of N linear equations with N unknowns:
Ax=bwhere:
- A is the coefficient matrix
- x is the column vector of unknowns
- b is the constant column vector
Step 1: Compute the Determinant of Matrix A
D=det(A)If D≠0 , the system has a unique solution.
Step 2: Compute Determinants for Modified Matrices
For each variable xi , replace the i-th column of A with vector b and compute the determinant:
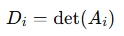
where Ai is the matrix A with its i-th column replaced by b.
Step 3: Compute Each Variable
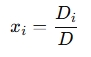
Example: Solving a 2×2 System Using Cramer’s Rule
Solve:
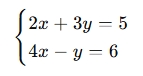
Step 1: Construct Coefficient Matrix A
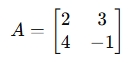
Compute det(A):
D=(2×(−1))−(3×4)=−2−12=−14Step 2: Replace Columns and Compute Determinants
For x, replace the 1st column with b:
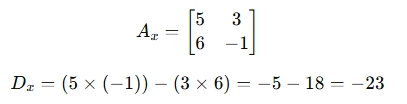
For y, replace the 2nd column with b:
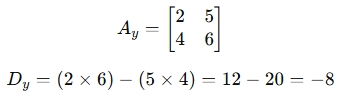
Step 3: Compute Solutions
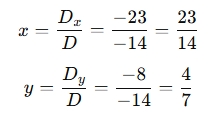
Final solution:
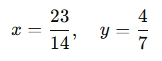
When to Use a Cramer’s Rule Determinant Calculator?
- When solving small systems (2×2, 3×3, or 4×4) of linear equations.
- When verifying manual solutions for linear equations.
- When determining if a system has a unique solution (det(A) ≠ 0) or no unique solution (det(A) = 0).
- When working with physics, engineering, or economics problems that involve linear relationships.