3x3 third-order matrix eigenvector calculator

Matrix A =
Scalar matrix (Z=c×I)=
|A| =
The trace of matrix A =
 
Singular matrix (A - c×I) =
 
|A - c×I| =
Eigenvalue c1 =
+ i
Eigenvalue c2 =
+ i
Eigenvalue c3 =
+ i
The value of c1 at the eigenvector (x,y,z) =
The value of c2 at the eigenvector (x,y,z) =
The value of c3 at the eigenvector (x,y,z) =

What is a 3×3 Third-Order Matrix Eigenvector Calculator?

A 3×3 Third-Order Matrix Eigenvector Calculator is a tool that finds the eigenvectors of a 3×3 matrix. Eigenvectors are special vectors that only get scaled (not rotated) when multiplied by the matrix.

For a 3×3 matrix:

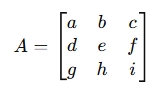
Eigenvectors v satisfy the equation:

Av=λv

where λ(lambda) are eigenvalues and v are the corresponding eigenvectors.

Why Use a 3×3 Eigenvector Calculator?

  1. Essential in Linear Algebra – Eigenvectors reveal fundamental properties of a matrix.
  2. Used in Many Applications:
    • Physics & Engineering – In quantum mechanics, stability analysis, and vibrations.
    • Computer Science & Machine Learning – Principal Component Analysis (PCA) uses eigenvectors for dimensionality reduction.
    • Economics & Data Science – For analyzing Markov processes and networks.
    • Graphics & Robotics – In image processing and transformations.

How Does It Work?

  1. Input a 3×3 matrix A.

  2. Find the Eigenvalues λ by solving the characteristic equation:

    det⁡(A−λI)=0

    where I is the identity matrix:

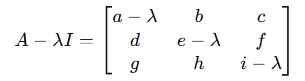
  3. Solve det⁡(A−λI)=0 to get the eigenvalues.

  4. Find eigenvectors by solving (A−λI)v=0 for each eigenvalue.

  5. Display the eigenvectors.