3x3 matrix determinant, adjoint matrix, inverse matrix calculator

Matrix(A)
Adjoint matrix (adj A)=
Determinant of a matrix (|A|) =
Inverse matrix = (adj A)/|A| =

A 3×3 Matrix Determinant, Adjoint, and Inverse Calculator is a tool used to compute the determinant, adjoint, and inverse of a given 3×3 matrix. These concepts are fundamental in linear algebra and have applications in various fields.

1. What Are These Concepts?

a) Determinant of a 3×3 Matrix

The determinant of a 3×3 matrix AA A is a scalar value that helps determine whether the matrix is invertible. It is calculated as:

det(A)=a(ei−fh)−b(di−fg)+c(dh−eg)

for a matrix:

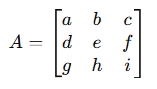
If det(A) = 0, the matrix is singular (not invertible).

b) Adjoint (Adjugate) Matrix

The adjoint (adjugate) matrix of A, denoted as adj(A), is the transpose of the cofactor matrix.

  • Each cofactor is computed by taking the determinant of a 2×2 minor matrix obtained by removing one row and one column.
  • Then, the cofactor matrix is transposed to form the adjoint.

c) Inverse of a 3×3 Matrix

The inverse of a matrix A, denoted as A−1, exists only if the determinant is nonzero. It is given by:

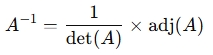
where:

  • det⁡(A) is the determinant.
  • adj(A) is the adjugate matrix.

2. Why Are These Important?

  • Determinant: Determines if a system of equations has a unique solution.
  • Adjoint: Helps in calculating the inverse and solving linear systems.
  • Inverse: Essential for solving equations of the form Ax=B , cryptography, transformations in graphics, etc.

3. How Does a Calculator Work?

  1. Input: A 3×3 matrix.
  2. Compute Determinant: Using the determinant formula.
  3. Compute Adjoint: By calculating cofactors and transposing them.
  4. Compute Inverse (if determinant ≠ 0):

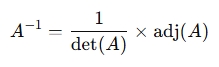
4. When to Use It?

  • When solving systems of linear equations.
  • When working with transformations in physics, computer graphics, and machine learning.
  • When manually computing determinants and inverses is time-consuming.