Transpose Matrix Calculator
|
| ||||||||||
| Results: | ||||||||||
| The transposed matrix of A = |
| |||||||||
What is a Transpose Matrix Calculator?
A Transpose Matrix Calculator is a tool used to compute the transpose of a given matrix. The transpose of a matrix is a new matrix obtained by flipping the matrix over its diagonal, turning its rows into columns and its columns into rows.
For example, given a matrix A:
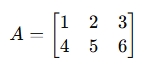
The transpose of matrix A, denoted AT, is:
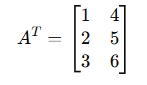
So the first row of A becomes the first column of AT, and similarly for the other rows and columns.
Why Use a Transpose Matrix Calculator?
- Simplifies Calculation – Saves time and effort when you need to transpose large matrices, especially in higher-dimensional problems.
- Matrix Operations – The transpose is essential for various matrix operations such as matrix multiplication, solving systems of equations, and finding inverses.
- Applications:
- In Linear Algebra – Used frequently in matrix factorization, eigenvalue problems, and other matrix-related tasks.
- In Physics & Engineering – For transformations, rotations, and analyzing systems.
- In Machine Learning – Used in algorithms involving vector and matrix operations, such as in neural networks.
- In Computer Graphics – Used for 3D transformations and projections.
How Does It Work?
-
Input a matrix.
-
Swap rows with columns. The element in the i-th row and j-th column of the original matrix becomes the element in the j-th row and i-th column of the transposed matrix.
If matrix A is of size m×n(i.e., m rows and n columns), then the transpose AT will be of size n×m.
Example Calculation
For a matrix A:
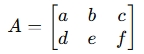
The transpose of matrix A, denoted AT, is:
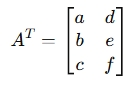
Here, the first row [a,b,c] becomes the first column, and the second row [d,e,f] becomes the second column.
When to Use It?
- In matrix multiplication – The transpose is used to change the orientation of matrices in multiplication operations.
- In machine learning – For operations involving data matrices and vectors, such as calculating dot products and applying transformations.
- In geometry and computer graphics – For transformations like rotations and projections in space.
- In systems of linear equations – The transpose is used in methods like the normal equation for solving least squares problems.