Continued Fraction Calculator
A Continued Fraction Calculator is a specialized tool that converts numbers into their continued fraction representations, offering a unique way to express real numbers as an iterative sequence of integer parts.
What Is a Continued Fraction Calculator?
-
Definition:
It’s a computational tool that takes an input number—whether a rational number (like 13/8) or an irrational number (like √2 or π)—and expresses it as a continued fraction. A continued fraction represents a number through a sequence such as: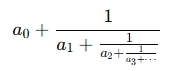
where a0 is the integer part and a1,a2,a3,… are the subsequent coefficients.
-
Output:
For a rational number, the expansion terminates (yielding a finite sequence), while for an irrational number, the sequence goes on indefinitely (often showing a periodic pattern in certain cases, such as quadratic irrationals).
Why Use a Continued Fraction Calculator?
-
Precision in Approximation:
Continued fractions provide some of the best rational approximations to irrational numbers. The convergents (the fractions obtained by truncating the continued fraction) are known to be excellent approximants. -
Insights into Number Properties:
They reveal the underlying structure of numbers. For instance, periodic continued fractions are linked to quadratic irrational numbers—a fact that has deep implications in number theory. -
Applications in Mathematics and Beyond:
- Number Theory: Helpful for solving Diophantine equations, like Pell’s equation.
- Cryptography: Sometimes used in cryptographic algorithms and in cryptanalysis.
- Educational Purposes: Assists students and educators in understanding the concept of convergence and number representations.
How Does It Work?
-
Algorithmic Process:
The typical method to convert a number into a continued fraction involves:-
Extracting the Integer Part:
Begin by identifying the integer part of the number, a0 . -
Subtract and Invert:
Subtract this integer part from the number to get the fractional remainder. Take the reciprocal of this remainder to form the next term. -
Iterative Calculation:
Repeat the process: for the new number obtained, extract its integer part, subtract it, and then invert the remainder. This continues until a desired accuracy is achieved or, in the case of a rational number, until the remainder becomes zero. -
Result Compilation:
The output is the list of integer coefficients [a0;a1,a2,a3,… ] that uniquely represents the original number.
-
-
Back-and-Forth Conversions:
Some calculators can also convert a given continued fraction back into a standard fraction or decimal, which is useful for verifying the approximation quality.
When to Use a Continued Fraction Calculator?
-
Analyzing Irrational Numbers:
When you need precise approximations of irrational numbers (such as in engineering or physics calculations), continued fractions offer excellent rational approximations. -
Number Theory and Research:
In academic research or advanced studies, continued fractions help explore the properties of numbers, solve equations, or understand periodicity in quadratic irrationals. -
Educational Settings:
Teachers and students can use these calculators to deepen their understanding of fractions, convergence, and the Euclidean algorithm. -
Practical Applications:
Beyond pure mathematics, they find utility in computer algorithms and cryptographic systems where precise approximations are crucial.