Pascal's Triangle Yang Hui's Triangle Calculator

Enter the number of rows in the Pascal's triangle (n) =
 

What Is a Pascal's Triangle (Yang Hui's Triangle) Calculator?

A Pascal's Triangle (Yang Hui's Triangle) Calculator is a tool used to generate Pascal's Triangle or Yang Hui's Triangle, which is a triangular array of numbers where each number is the sum of the two numbers directly above it. It’s named after Blaise Pascal, a French mathematician, though it was known in China as Yang Hui's Triangle after the Chinese mathematician Yang Hui.

This triangle is a powerful tool in mathematics and is used in various areas like combinatorics, algebra, and binomial expansions.

Why Use a Pascal's Triangle (Yang Hui's Triangle) Calculator?

  1. Binomial Expansions – Pascal’s Triangle provides the coefficients of the expanded form of a binomial expression (e.g., (x+y)n).
  2. Combinatorics – It helps in calculating binomial coefficients, which are essential for problems in probability, combinatorics, and statistics.
  3. Mathematical Education – It’s a helpful tool for understanding sequences, patterns, and basic algebra, making it popular in teaching environments.
  4. Efficient Calculation – Instead of calculating binomial coefficients manually, the calculator helps generate the necessary rows of the triangle quickly.
  5. Fibonacci Sequence – The triangle can also be used to observe relationships in other mathematical sequences, such as the Fibonacci sequence.
  6. Summing Numbers – Each number in the triangle is a sum of the two numbers above it, helping with understanding sequences and summation.

How Does It Work?

Pascal's Triangle is constructed row by row. Each row corresponds to the coefficients of the expanded binomial expression (x+y)n, where n is the row number, starting from 0.

  1. The first row is just a 1.
  2. The second row is 1, 1.
  3. The third row is 1, 2, 1, because the middle number is the sum of the two numbers above it (1 + 1 = 2).
  4. The fourth row is 1, 3, 3, 1, where the middle numbers are the sums of the numbers directly above them (1 + 2 = 3, and 2 + 1 = 3).
  5. And so on...

The general rule for creating a row is:

  • The first and last numbers of each row are always 1.
  • The other numbers are the sum of the two numbers directly above them from the previous row.

Example:

The first few rows of Pascal’s Triangle are:

Row 0:      1
Row 1:     1  1
Row 2:    1  2  1
Row 3:   1  3  3  1
Row 4:  1  4  6  4  1
Row 5: 1  5  10  10  5  1

Formula to Generate Binomial Coefficients:

Each number in the triangle is a binomial coefficient, denoted as C(n,k), where n is the row number and k is the position in that row (starting from 0).

The general formula for C(n,k) is:

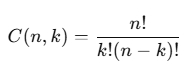
Where n! is the factorial of n, and k! is the factorial of k.

When to Use a Pascal's Triangle (Yang Hui's Triangle) Calculator?

  1. Binomial Expansion – When you need the coefficients for expanding binomial expressions such as (x+y)n. For example, the expansion of (x+y)3 can be found using row 3 of Pascal’s Triangle: 1, 3, 3, 1.
  2. Combinatorics Problems – In problems where you need to compute combinations, Pascal’s Triangle is a quick way to find values of binomial coefficients.
  3. Mathematical Education – To visually demonstrate concepts like sequences, binomial expansions, or recursive patterns in teaching.
  4. Data Analysis and Probability – Pascal’s Triangle can help in calculating probabilities or organizing large data sets, especially when dealing with combinations.
  5. Fibonacci Sequence – You can observe relationships to Fibonacci numbers through certain diagonals in Pascal’s Triangle.