Percent Calculator
| What is | % of |
| Result = | |
What Is a Percent Calculator?
A Percent Calculator is a tool that helps you calculate percentages. It allows you to quickly find a percentage of a number, determine what percentage one number is of another, or solve for unknown values in percentage-related problems. It can perform a variety of operations such as finding percentages, calculating percentages of numbers, and solving percentage-based equations.
For example:
- What is 20% of 150?
- What percentage of 50 is 10?
- If you know a number is 20% of another number, what is the full number?
Why Use a Percent Calculator?
- Quick Calculations – It speeds up the process of calculating percentages, which can otherwise be time-consuming.
- Accuracy – It ensures that the percentage calculation is correct, eliminating human error.
- Common in Everyday Life – Percentages are used frequently in daily activities such as discounts, taxes, tips, interest rates, and profit margins.
- Business and Finance – Percent calculations are crucial for financial analysis, sales calculations, budgeting, and more.
- Education – It helps students or anyone learning about percentages and their application in various fields of study.
How Does It Work?
A percent represents a value out of 100. To calculate a percentage, follow these common formulas:
-
Finding a Percentage of a Number:
- Formula:
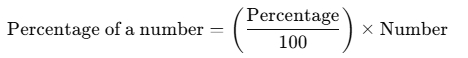
- Example: What is 20% of 150?
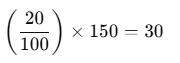
So, 20% of 150 is 30.
- Formula:
-
Finding What Percentage One Number is of Another:
- Formula:
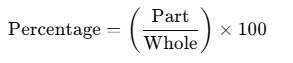
- Example: What percentage of 50 is 10?
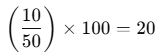
So, 10 is 20% of 50.
- Formula:
-
Finding the Total From a Given Percentage:
- Formula:
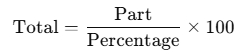
- Example: If 20% of a number is 30, what is the total number?
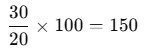
So, the total number is 150.
- Formula:
When to Use a Percent Calculator?
- Shopping and Discounts – To calculate the discount on a product (e.g., 25% off a $100 item).
- Financial Calculations – To calculate interest rates, tax percentages, or profit margins (e.g., determining the interest on a loan or the percentage return on an investment).
- Tip Calculation – To calculate tips (e.g., 15% tip on a restaurant bill).
- Grade Calculations – To calculate exam or class grades based on percentages.
- Sales and Marketing – To analyze sales data and determine percentage increases or decreases.
- Comparative Analysis – When comparing parts of a whole, for example, comparing performance metrics or sales growth.