Pythagorean Theorem Calculator
What is a Pythagorean Theorem Calculator?
A Pythagorean Theorem Calculator is a tool used to calculate the lengths of the sides of a right triangle based on the Pythagorean theorem. The Pythagorean theorem is a fundamental principle in geometry that applies to right-angled triangles, stating that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
The formula for the Pythagorean theorem is:
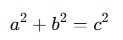
Where:
- a and b are the lengths of the two legs (the sides that form the right angle),
- c is the length of the hypotenuse.
Why is the Pythagorean Theorem Important?
- Geometry and Trigonometry: It’s one of the most important principles in geometry, widely used in trigonometry, construction, and various fields of mathematics.
- Real-Life Applications: It helps in various real-world scenarios like building design, navigation, and even computer graphics.
- Calculating Distance: The theorem is used to calculate distances in 2D space, such as finding the shortest distance between two points or the distance traveled along a straight path.
- Basis for Other Theorems: It is foundational for proving other mathematical concepts and theorems.
How Does a Pythagorean Theorem Calculator Work?
The Pythagorean theorem calculator helps find the missing side of a right triangle when given the lengths of two sides. It can work in the following ways:
-
Finding the Hypotenuse (c): If you know the lengths of the two legs (a and b), the calculator can find the hypotenuse using the formula:
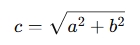
-
Finding a Leg (a or b): If you know the hypotenuse (c) and one leg (a or b), the calculator can find the missing leg using the formula:
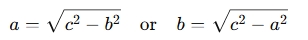
-
Step-by-Step Calculation: The calculator will often show the calculation steps and provide the result, allowing you to understand how the missing side is calculated.
Why Use a Pythagorean Theorem Calculator?
- Quick and Easy Calculation: It simplifies finding the length of a side in a right triangle, which can be tedious and time-consuming if done manually.
- Error-Free: It eliminates the risk of making calculation errors by providing accurate results instantly.
- Convenient for Students: It's a helpful tool for students learning geometry, as it aids in visualizing and solving problems related to right triangles.
- Real-World Applications: It's useful in practical fields like construction, engineering, architecture, navigation, and more, where accurate measurements and distances are required.
How to Use a Pythagorean Theorem Calculator?
- Input Values: Enter the lengths of the known sides of the triangle (two of the sides).
- Choose the Unknown Side: Depending on which side is unknown (hypotenuse or one leg), the calculator will use the appropriate formula.
- Calculation: The calculator will perform the necessary mathematical operations and display the result.
- Step-by-Step Explanation: Some calculators will also show you how they arrived at the result, breaking down the formula and calculations for you.
When to Use a Pythagorean Theorem Calculator?
- Right Triangle Problems: Use it when you need to find the length of one side of a right triangle, whether for school assignments, homework, or test preparation.
- Construction and Design: It’s used in real-world applications such as measuring distances for building projects, where precision is important, and a right triangle is involved.
- Distance Calculations: In navigation, whether in a 2D map or 3D space, the Pythagorean theorem can help you calculate straight-line distances.
- Physics and Engineering: It’s used in various fields of physics and engineering where the calculation of distances or lengths in right-angled situations is required.
- Geometry Practice: When practicing or learning geometry, this calculator is an excellent tool for quick verification of your calculations.