Tetrahedron number, triangular pyramid number calculator

Non-negative number (n) =
 
Tetrahedron number, triangular pyramid number (Tn) =

A Tetrahedron Number (or Triangular Pyramid Number) Calculator is a tool used to calculate numbers in a sequence known as tetrahedral numbers, which represent the number of objects that can form a three-dimensional pyramid with a triangular base. These numbers are part of a broader class of polygonal pyramid numbers, where each shape's base is a polygon.

What is a Tetrahedron Number?

A Tetrahedron number (or triangular pyramid number) is the total number of objects that can form a pyramid with a triangular base. The formula to find the nth tetrahedral number is:

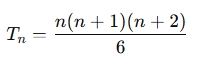
Where:

  • Tn​ is the nth tetrahedron number.
  • n is a positive integer (the position in the sequence).

The first few tetrahedral numbers are:

  • T1=1(a single point)
  • T2=4 (a pyramid with 3 points in the base and 1 on top)
  • T3=10
  • T4=20
  • T5=35
  • T6=56, and so on.

Why use a Tetrahedron Number Calculator?

The tetrahedron number sequence arises in various mathematical contexts, especially in combinatorics, geometry, and number theory. Using a calculator for these numbers helps when dealing with problems or patterns involving triangular pyramids, for example:

  • To compute the number of points in a three-dimensional pyramid or stacked objects.
  • To explore properties in combinatorial mathematics.
  • To solve geometry-related problems where pyramid-like structures are considered.

How does it work?

A Tetrahedron Number Calculator uses the formula mentioned above to compute the nth tetrahedral number. The steps include:

  1. Taking an input value nn n (the number in the sequence you want).
  2. Plugging n into the formula .
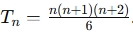  3. Returning the calculated value, which represents the nth tetrahedron number.

When would you use it?

You would use a Tetrahedron Number Calculator when:

  • You need to calculate a specific tetrahedron number for a particular sequence.
  • You're working with problems involving stacked triangular pyramids or similar three-dimensional figures.
  • You're analyzing combinatorial or geometric properties that relate to three-dimensional objects with triangular bases.