Sector, chord, arc length calculator

Choose two parameters you know
Radius and center angle    Radius and chord AB
Radius and ridge ED    Radius and apicocenter distance OE
Radius and chord AB
Chord AB and arc ED    Chord AB & Aperture OE
Aperture ED & Aperture OE    Chord AB & Arc AB



Number of effective digits >>>

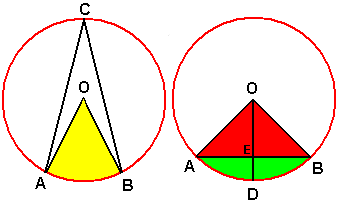
AO and OB are called radii

AC, BC and AB are called chords

Angle ACB is the circular angle

Angle AOB is the center image

The curved part of AB is the arc.

OE is the apicocenter distance

Triangle AOB is the triangular area

ED is the arch height

The arc length calculation formula is: (Central Angle / 180°) •π • r

The yellow area is the sector

The sector area formula is: (Angle AOB / 360°) •π • r²

The green area is the arch height area

This area size = sector area - AOB triangle

A sector, chord, and arc length calculator is a tool that helps calculate various properties of a circle or a circular segment, based on input parameters such as the angle of the sector, the radius, or the length of the chord. It provides results for the following:

  1. Sector: A sector of a circle is the region enclosed by two radii and the arc between them. It's like a "slice" of a circle. The area and perimeter of a sector can be calculated if you know the radius and the central angle of the sector.

  2. Chord: A chord is a straight line connecting two points on the circle. It's not a part of the circumference but a line segment that cuts through the circle. The length of a chord can be calculated from the radius and the central angle.

  3. Arc Length: The arc length is the distance along the curved part of a circle between two points on the circumference. It depends on the radius of the circle and the central angle between the points.

Why You Need It:

These calculations are useful in various fields such as geometry, physics, engineering, architecture, and even in real-world applications like navigation, design, and construction. For instance:

  • Understanding circular motion.
  • Designing mechanical parts like gears or wheels.
  • Determining the length of cable around a circular path.

When You Use It:

You would use such a calculator when you have some of the key information (like the radius and central angle) and need to find other missing properties (such as the arc length, chord length, or sector area). For example, you might use it to:

  • Determine how much material is needed to cover a portion of a circular surface.
  • Calculate the distance along a curved road or track (arc length).
  • Find the distance between two points on a circle (chord).