Hyperbola Calculator
A hyperbola is the locus of points whose absolute value of the difference between the distance to two fixed points on a plane is a constant. It can also be defined as the locus of points whose ratio of the distance to a fixed point to a fixed line is a constant greater than 1. A hyperbola is a type of conic section, i.e., the intersection of a cone and a plane. Hyperbola a²+b²=c²
Hyperbola Equation Calculator
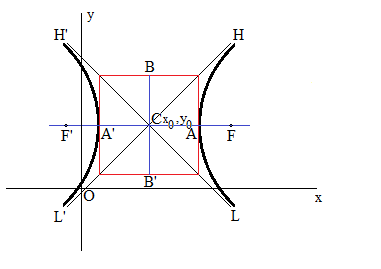
Hyperbola Focus F X-axis= x0 + √(a2 + b2)
Hyperbola Focus F Y-axis= y0
Hyperbola Focus F' X-axis = x0 - √(a2 + b2)
Hyperbola Focus F' Y axis = y0
Asymptote H'L: y=(b/a)x + y0 - (b/a)x0
Asymptote LH': y=(-b/a)x + y0 + (b/a)x0
Hyperbola eccentricity = √(a2 + b2)/a
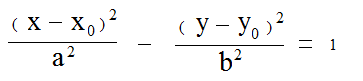
A Hyperbola Calculator is a tool that helps you analyze and compute properties of a hyperbola, which is a type of conic section. Hyperbolas are curves formed by the intersection of a double cone with a plane.
The properties of a hyperbola, like its center, foci, vertices, and asymptotes, can be computed using this equation.
Why use a Hyperbola Calculator?
A Hyperbola Calculator is useful because:
- Quick Calculation: It helps compute key properties of a hyperbola without requiring complex manual calculations.
- Visualization: Some calculators allow you to graph the hyperbola, making it easier to understand the shape and behavior of the curve.
- Problem Solving: It's particularly useful for students and professionals dealing with geometry, physics, engineering, and other fields that require understanding hyperbolas.
How does a Hyperbola Calculator work?
The calculator works by taking the equation of the hyperbola or the coordinates of key points (such as the center, foci, and vertices), and then applying the relevant formulas to compute:
- Center: The midpoint of the hyperbola.
- Vertices: The points where the hyperbola intersects the axis.
- Foci: The two fixed points used to define the hyperbola.
- Asymptotes: The lines the hyperbola approaches but never touches.
- Eccentricity: A measure of how "stretched" the hyperbola is.
When to use a Hyperbola Calculator?
You should use a Hyperbola Calculator:
- When studying hyperbolas in conic sections.
- When solving geometry problems related to hyperbolas.
- When you need to quickly compute and understand properties of hyperbolas for academic or professional purposes.