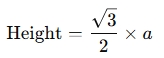Isosceles (equilateral) triangle calculator

Side a Side b
Angle A Angle B
Area:
Perimeter:
Radius of circumscribed circle:
Radius of inscribed circle:
Height of side a:
Height of side b:
Angle bisector of side a:
Angle bisector of side b:
Medium bisector of side a:
Medium bisector of side b:

Area (K) K2 = b2 * (4 × a2 - b2) / 16
Perimeter 2 × a + b
Angle bisector of side b ( tb ) tb2 = 4 × a2 - b2 / 2
Angle bisector of side a ( tb ) ta2 = b2 × a × (2a + b) / (a ​​+ b)2
Median of side a ( ma ) ma2 = (2 * b2 + a2) / 4
Side b midline ( mb ) mb2 = (4 * a2 - b2) / 4
Circumscribed circle radius a / ( 2 * sin (A)) or b / ( 2 * sin (B))
Inscribed circle radius (r) r2 = b2 × (2a - b) / (4 × (2a + b))

An Isosceles (Equilateral) Triangle Calculator is a tool designed to help you compute various properties of isosceles and equilateral triangles. These types of triangles have specific geometric properties that make them easier to analyze with the help of a calculator.

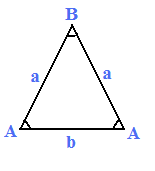
Isosceles Triangle:

An isosceles triangle is a triangle with two equal sides. The angles opposite these equal sides are also equal.

Equilateral Triangle:

An equilateral triangle is a special case of an isosceles triangle where all three sides are equal. Therefore, all the interior angles are equal and each measures 60 degrees.

Why use an Isosceles (Equilateral) Triangle Calculator?

A calculator for these triangles is useful because:

  1. Quick and Accurate Calculations: It helps you calculate key properties, such as side lengths, angles, area, and height, without performing lengthy manual calculations.
  2. Visualization: Some calculators can also provide graphical representations of the triangle.
  3. Time-Saving: It saves time when solving geometry problems, especially when there are many similar shapes or multiple steps involved.
  4. Educational Purpose: It can help students or anyone learning geometry to verify their answers and understand the relationships between the sides and angles of the triangle.

How does the Isosceles (Equilateral) Triangle Calculator work?

For an isosceles triangle, the calculator can compute the following properties:

  1. Side Lengths: Given the equal sides or the base, the calculator can determine the lengths of all sides.
  2. Angles: If the base angle is known, the calculator can find the other angles, or vice versa.
  3. Area: The area can be calculated using formulas like: Area=1/2×Base×Height
  4. Height: The height (altitude) can be calculated based on the base and side lengths.

For an equilateral triangle, the calculator can quickly determine:

  1. Side Length: All sides are equal, so knowing one side gives you all the other side lengths.
  2. Angles: All angles are 60° in an equilateral triangle.
  3. Area: The area of an equilateral triangle is given by:

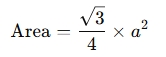
    where a is the length of a side.
  4. Height: The height of an equilateral triangle can be computed as: