Parabola Equation Solver Calculator
When the vertex of the parabola equation is (h, k) and the focus is (x1, y1), then the vertex equation of the parabola is:
(X-h)2 = 4a(Y-k); ( a = √(h-x1) * (h-x1) + (k - y1) * (k-y1) )
Standard form of the parabola equation:
Y = (1/4a)X2 - (h/2a)X + (k + h2/4a); ( a = √(h-x1) * (h-x1) + (k - y1) * (k-y1) )
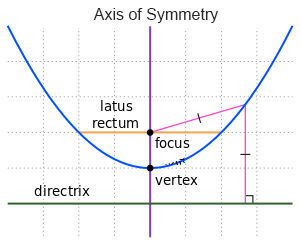
A Parabola Equation Solver Calculator is a tool that helps you solve equations of parabolas and calculate important properties related to them, such as their vertex, focus, directrix, and more. Parabolas are U-shaped curves that are commonly seen in algebra and geometry, especially in quadratic equations.
What is a Parabola?
A parabola is a symmetric curve that represents the graph of a quadratic function. The general equation for a parabola is:
- Standard Form (vertical parabola): y=ax2+bx+c
- Vertex Form (easy to identify vertex): y=a(x−h)2+k where (h, k) is the vertex of the parabola.
A parabola can open upwards, downwards, left, or right, depending on the equation. The direction of the opening and the properties of the parabola are determined by the coefficients in the equation.
Why use a Parabola Equation Solver Calculator?
A Parabola Equation Solver Calculator is useful because:
- Quick Calculation: It simplifies the process of solving equations and finding important features of the parabola without needing to do complex manual calculations.
- Convenience: It is especially helpful when working with large, complicated numbers or needing multiple computations for a single parabola (e.g., finding its vertex, focus, and directrix).
- Visualization: Many calculators provide graphical representations, so you can visually understand the shape and features of the parabola.
- Accuracy: It eliminates the risk of errors in calculations when solving quadratic equations or working with parabola-related properties.
How does a Parabola Equation Solver Calculator work?
The calculator works by taking the equation of a parabola (usually in standard form or vertex form) and then applying the following calculations:
- Vertex: In the equation y=ax2+bx+c , the vertex can be found using the formula:
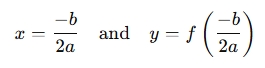
- Focus: The focus is a point inside the parabola that lies on the axis of symmetry. For a vertical parabola, it is given by:
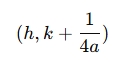
- Directrix: The directrix is a line that is perpendicular to the axis of symmetry. For a vertical parabola, it is given by:
- Equation of the Parabola: If you are given certain properties (such as the vertex or focus), the calculator can also work backward to find the equation of the parabola.
- X-Intercepts and Y-Intercept: The calculator can also help find the points where the parabola intersects the axes.
When to use a Parabola Equation Solver Calculator?
You should use this calculator:
- Solving Quadratic Problems: When you're working on problems that require solving quadratic equations or working with the properties of parabolas.
- Verifying Solutions: If you've manually solved for the vertex, focus, or directrix, you can use the calculator to check your work.
- Graphing: If you need to quickly graph a parabola, the calculator might help you plot it by calculating key points like the vertex and intercepts.
- Understanding Parabolas: If you're learning about parabolas and need to explore different aspects of the shape, such as its orientation, focus, or how it changes with different coefficients.
- Optimization Problems: In physics or engineering, parabolas are used to model projectile motion, and the calculator can help in finding optimal values (like maximum height or range).