Parallelogram, Square, Rhombus, Rectangle Calculator

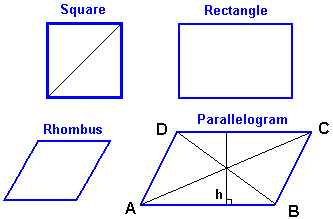
In plane geometry, a square is a polygon with four equal sides and four equal interior angles. A square is a regular polygon, also known as a regular quadrilateral. Each interior angle is a right angle, that is, 90 degrees.

In geometry, a rectangle (also known as a rectangle) is defined as a quadrilateral with four equal interior angles, that is, all interior angles are right angles. From this definition, it can be concluded that the two opposite sides of a rectangle are of equal length, that is, a rectangle is a parallelogram. A square is a special case of a rectangle, and its four sides are of equal length. At the same time, a square is both a rectangle and a rhombus.

In a plane, a parallelogram with a set of equal adjacent sides is a rhombus.

A quadrilateral with two sets of equal angles in the same plane is called a parallelogram.

A Parallelogram, Square, Rhombus, and Rectangle Calculator is a tool or software designed to assist with calculating properties of these four types of quadrilaterals. Each of these shapes has unique geometric properties, and such a calculator can help in determining various aspects like area, perimeter, side lengths, angles, and diagonals.

Here’s an explanation of each part:

What is a Parallelogram, Square, Rhombus, Rectangle Calculator?

It is a tool or application that helps calculate different properties of four types of quadrilaterals:

Parallelogram: A four-sided figure where opposite sides are parallel and equal in length.
Square: A special case of a rectangle where all sides are equal, and all angles are right angles (90°).
Rhombus: A type of parallelogram where all sides are of equal length, but the angles are not necessarily 90°.
Rectangle: A parallelogram with right angles, where opposite sides are equal in length.

This calculator typically helps you calculate properties such as area, perimeter, diagonals, and side lengths using the given inputs (e.g., side length, angle, diagonal length).

Why Use a Parallelogram, Square, Rhombus, Rectangle Calculator?

You would use this kind of calculator for several reasons:

Quick and Accurate Calculations: It provides fast and accurate calculations without having to do the math manually, especially for properties like area, perimeter, and angles.
Educational Tool: Helps students and teachers in understanding the relationships between different quadrilaterals and their properties.
Problem Solving: Makes solving geometry problems easier, especially when the problem involves complex shapes and multiple properties.
Real-Life Applications: Can be used in fields like architecture, engineering, and design where knowledge of these shapes is essential for planning and creating objects or structures.

How Does the Calculator Work?

This calculator works by taking inputs such as:

Side lengths (for squares, rectangles, rhombuses, and parallelograms)
Angles (in degrees, usually for rhombuses or parallelograms)
Diagonals (lengths of diagonals in some shapes)
Area (you can input one known dimension like side or angle to calculate the area)

Once you input the known information, the calculator uses mathematical formulas for each shape to compute the unknown properties. Here’s how the formulas typically work:

For a Parallelogram:

Area: Area=base×height
Perimeter: Perimeter=2×(base+side)

For a Square:

Area: Area=side²
Perimeter: Perimeter=4×side
Diagonal: Diagonal=side×√2

For a Rhombus:

Area: Area=1/2×diagonal1×diagonal2
Perimeter: Perimeter=4×side
Diagonal Lengths: Can be derived from the sides and angles using trigonometry.

For a Rectangle:

Area: Area=length×width
Perimeter: Perimeter=2×(length+width)
Diagonal: Diagonal=

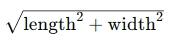
When to Use a Parallelogram, Square, Rhombus, Rectangle Calculator?

You would use this calculator when:

Solving Geometry Problems: When you need to calculate areas, perimeters, or angles for any of these quadrilaterals.
Learning Geometry: In educational settings for visualizing and calculating different properties of quadrilaterals.
Designing or Engineering: When working with structures or designs that involve geometric shapes like squares or rectangles, and you need quick measurements.
Real-World Applications: For instance, calculating the area of a rectangular field, the perimeter of a rhombus-shaped piece of material, or the square footage of a floor.