Spherical cap volume and surface area calculator

Radius (r):
Height of the spherical cap (h):
Volume of the spherical cap:
Surface area of ​​the spherical cap:

Spherical crown calculation formula：

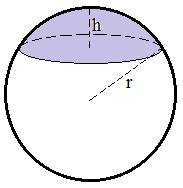
1. Sphere volume = 4 * π * r3 / 3
2. Sphere surface area = 4 * π * r2
3. Spherical cap volume = π * h2 * (3r - h) / 3
4. Spherical cap surface area = 2 * π * r * h

A spherical cap is a portion of a sphere that is "cut off" by a plane. It refers to the upper or lower segment of a sphere, not the entire sphere. The spherical cap has two key properties that can be calculated: its volume and surface area.

1. What is a Spherical Cap?

A spherical cap is the portion of a sphere above (or below) a given plane. The height of the cap is the distance from the plane to the top of the spherical cap. The base of the spherical cap is the circle formed by the intersection of the sphere and the plane.

2. Why is it Important?

Calculating the volume and surface area of a spherical cap is useful in various fields such as:

  • Physics: To calculate properties of spherical objects like lenses, segments of tanks, or domes.
  • Engineering: For designing parts of machines, structural elements, or in fluid mechanics.
  • Astronomy: For understanding the geometry of spherical objects like planets or moons.
  • Geometry: For academic purposes and practical applications in measuring sections of spheres.

3. How is the Volume and Surface Area Calculated?

  • Volume of a Spherical Cap: The formula for the volume of a spherical cap is:

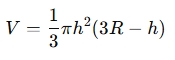
Where:

  • V is the volume of the spherical cap,

  • h is the height of the spherical cap,

  • R is the radius of the sphere.

  • Surface Area of a Spherical Cap: The formula for the surface area of a spherical cap is:

A=2πRh

Where:

  • A is the surface area of the spherical cap,
  • R is the radius of the sphere,
  • h is the height of the spherical cap.

4. When is the Spherical Cap Volume and Surface Area Used?

You would use these calculations in scenarios like:

  • Designing spherical containers or domes where only a segment of the sphere is used.
  • Understanding lens geometry in optical physics.
  • Calculating volumes for liquid storage where the shape is part of a spherical tank.
  • Simulating astronomical objects like a planetary segment.

5. Using a Spherical Cap Volume and Surface Area Calculator

A spherical cap calculator allows you to input values for the radius R and height h, and it computes the volume and surface area quickly. It's useful because the calculations can be complex and might require multiple steps, especially when you're working with spherical geometry in practical applications.