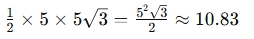30 60 90 Right Triangle Calculator

Instructions: Enter a number and click "Calculate"!

Long side:
Short side:
Hypotenuses:
Area:
Perimeter:

A 30-60-90 Right Triangle Calculator is a tool specifically designed to help solve problems involving 30-60-90 right triangles. These triangles have one angle of 30°, one angle of 60°, and a right angle (90°). This type of triangle is a special case of right triangles that allows for quick calculations of the sides based on their specific geometric properties.

Why Use a 30-60-90 Right Triangle Calculator?

In a 30-60-90 triangle, the ratio of the sides is always fixed, which makes it easy to solve for unknown sides given one known side. A 30-60-90 calculator simplifies the process of solving such triangles, saving time and reducing the chance of errors. It's especially useful in:

  • Geometry classes for students
  • Engineering or architectural design, where 30-60-90 triangles are often used
  • Land surveying or construction, when dealing with triangular plots or shapes

How Does it Work?

In a 30-60-90 right triangle, the sides have a specific ratio:

  • The side opposite the 30° angle is the shortest side (often labeled x).
  • The side opposite the 60° angle is x√3 ​ (the longer leg).
  • The side opposite the 90° angle is the hypotenuse, which is 2x (twice the shortest side).

Using the Calculator:

  1. Input one side: If you know one side of the triangle, you can easily calculate the others using the ratios.

    • If you know the shortest side xx x, you can calculate the other two sides:
      • The longer leg (opposite the 60° angle) = x√3
      • The hypotenuse (opposite the 90° angle) = 2x
    • If you know the hypotenuse (which is twice the shortest side), you can find the other sides by halving the hypotenuse for the shortest side and using the ratio to find the longer leg.
    • If you know the longer leg, divide it by √3 ​ to find the shortest side and use that to find the hypotenuse.

  2. Formula for the area: The area of a 30-60-90 triangle is simply:

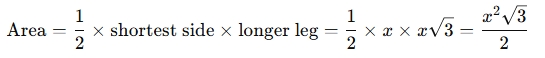
The calculator will use these relationships to quickly compute the missing sides or area of the triangle when you provide one known value.

When Should You Use it?

You should use a 30-60-90 Right Triangle Calculator:

  • When dealing with 30-60-90 triangles: If you encounter a right triangle with angles of 30°, 60°, and 90°, you can use this tool to quickly solve for unknown sides.
  • In math and geometry classes: If you're studying trigonometry or geometry and need to solve for side lengths and areas of 30-60-90 triangles, this calculator can be very helpful.
  • In real-world applications: When working with triangles in construction, design, and engineering, this type of triangle is common due to its predictable properties.

Example:

  • Given the shortest side x=5 :
    • The longer leg (opposite the 60° angle) = 5√3≈8.66
    • The hypotenuse (opposite the 90° angle) = 2×5=10
    • The area of the triangle =