Parallelogram Calculator

Basea：
Baseb：
Height (h)：
Angle (θ)：
Area:
Perimeter:
Short diagonal:
Long diagonal:
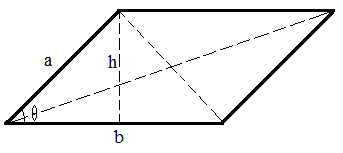
1. Area = bh = absinθ

2. Perimeter = 2a + 2b

3. Short diagonal = sqrt(a2 + b2 - 2abcos(θ));

4. Long diagonal = sqrt(a2 + b2 - 2abcos(π - θ));

A Parallelogram Calculator is a tool that helps you compute various properties of a parallelogram, a type of quadrilateral. A parallelogram has opposite sides that are both equal and parallel. This tool can calculate key features of a parallelogram such as area, perimeter, side lengths, angles, and diagonals, based on the information you provide.

What is a Parallelogram?

A parallelogram is a quadrilateral (a four-sided polygon) where:

  • Opposite sides are parallel and equal in length.
  • Opposite angles are equal.
  • The diagonals bisect each other (they divide each other into two equal parts).

Common types of parallelograms include:

  1. Rectangle: A parallelogram with right angles.
  2. Rhombus: A parallelogram with all sides of equal length.
  3. Square: A special case of a rectangle and a rhombus, where all sides are equal, and all angles are right angles.

Why use a Parallelogram Calculator?

A Parallelogram Calculator is useful because:

  1. Quick Calculations: It saves time by quickly calculating important properties like area, perimeter, angles, or the length of diagonals without needing to manually perform the complex steps.
  2. Problem Solving: It is particularly useful for geometry students, engineers, architects, and anyone working with parallelograms in their calculations or designs.
  3. Accuracy: The calculator ensures that calculations are done correctly, reducing the chances of mistakes in solving problems.
  4. Efficiency: When dealing with multiple parallelograms or repeated calculations, it provides an efficient way to solve geometric problems.

How does a Parallelogram Calculator work?

The calculator works by using the geometry formulas specific to parallelograms. Based on the information provided (such as side lengths, angles, or diagonal lengths), the calculator applies these formulas:

  1. Area: The area of a parallelogram can be calculated as:

    Area=Base×Height

    where the base is the length of one of the sides, and the height is the perpendicular distance between the parallel sides.

  2. Perimeter: The perimeter of a parallelogram is calculated by adding the lengths of all four sides:

    Perimeter=2×(Base+Side Length)

  3. Angles: If one angle is known, the calculator can compute the other angle (since opposite angles in a parallelogram are equal). Adjacent angles are supplementary, so their sum is 180°.

  4. Diagonals: If the lengths of the sides and an angle are known, the calculator can compute the lengths of the diagonals using the formula derived from the law of cosines:

    Diagonal 12=Side 12+Side 22−2×Side 1×Side 2×cos⁡(θ)

    where θ\theta θ is the angle between the two sides.

  5. Side Lengths: If the area and height are provided, the calculator can solve for the unknown side length using the formula for area.

When to use a Parallelogram Calculator?

You should use a Parallelogram Calculator when:

  1. Solving Geometry Problems: If you're working with parallelograms in a geometry class or doing math exercises that involve finding area, perimeter, or angles.
  2. Designing and Engineering: Architects or engineers working with parallelogram shapes (such as in trusses or designs) can use the calculator to quickly solve for dimensions.
  3. Checking Work: After solving for properties like area or perimeter by hand, you can use the calculator to verify your answers.
  4. Optimization: When you're working with designs that involve parallelograms, the calculator can help you quickly adjust dimensions to meet specific criteria (like area or perimeter).
  5. Visualizing and Exploring: If you're learning or teaching geometry, using a calculator can help visualize how changing one property of the parallelogram (like an angle or side length) affects the other properties.

In Summary:

A Parallelogram Calculator is a highly efficient tool for solving problems related to parallelograms in geometry. It simplifies the process of calculating important properties such as area, perimeter, and diagonals, and is helpful in both educational and practical contexts. Whether you're studying, solving real-world problems, or designing, this calculator helps you quickly and accurately find the needed information.