Arccosine function calculator

arccos    

y=arccos(x) Graph

Y
(Degrees)		 Y
(Radian)		 X
180 ̊ π -1
150 ̊ 5π/6 -0.866025
135 ̊ 3π/4 -0.707107
120 ̊ 2π/3 -0.5
90 ̊ π/2 0
60 ̊ π/3 0.5
45 ̊ π/4 0.707107
30 ̊ π/6 0.866025
0 ̊ 0 1

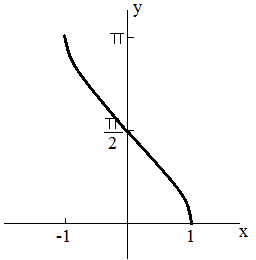
What is an Arccosine (Inverse Cosine) Function Calculator?

An Arccosine Function Calculator is a tool used to compute the inverse cosine of a given number, denoted as arccos(x) or cos⁡−1(x). The arccosine function returns the angle whose cosine is a given value. The result is usually expressed in radians or degrees within the domain of [0,π] radians (or [0∘,180∘]).

The formula for the inverse cosine function is:

arccos(x)=cos⁡−1(x)

where the domain is −1≤x≤1, because the cosine of any angle can only produce values within this range.

Why Use an Arccosine Function Calculator?

  • Quick and accurate results: It provides the angle that corresponds to a given cosine value instantly, saving time and reducing the potential for errors.
  • Solves trigonometric equations: It helps find angles when the cosine value is known, often used in geometry, physics, and engineering.
  • Convenience: It avoids manually solving complex trigonometric equations or using trigonometric tables.
  • Essential for certain applications: Useful in any field where angles and their relationships to cosine values are important.

How Does an Arccosine Function Calculator Work?

  1. Input a value: The calculator requires a value of xx x, where −1≤x≤1, as cosine values are limited to this range.
  2. Apply the inverse cosine formula: The calculator computes the angle θ such that cos⁡(θ)=x.
    • The result is expressed in either radians or degrees, depending on your settings.
    • The value returned is typically between 0 and π radians (or between 0° and 180°).
  3. Display the result: The angle (in radians or degrees) corresponding to the given cosine value is shown.

When to Use an Arccosine Function Calculator?

  • In geometry: When solving for angles in triangles, especially in cases where the cosine of an angle is known.
  • In physics: To calculate angles in wave motion, forces, or rotational motion, where the cosine function is involved.
  • In engineering: In problems involving trigonometry, such as in structural analysis, signal processing, or electrical engineering.
  • In navigation and astronomy: To find angles or directions based on known distances or velocities, where trigonometric functions come into play.
  • In computer graphics: For transformations, rotations, and rendering angles in 3D space.