Tangent function calculator

x:
=
Tangent (x):

y=tangent(x) Graph

X
(deg)		 X
(Rad)		 tangent(X)
180 ̊ π 0
150 ̊ 5π/6 -0.57735
135 ̊ 3π/4 -1
120 ̊ 2π/3 -1.732051
90 ̊ π/2 Out of Range
60 ̊ π/3 1.732051
45 ̊ π/4 1
30 ̊ π/6 0.57735
0 ̊ 0 0

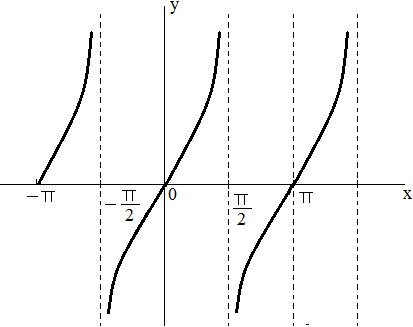
What is a Tangent Function Calculator?

A Tangent Function Calculator computes the tangent (tan) of a given angle. The tangent function is a fundamental trigonometric function defined as:

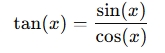
where x is the angle (in degrees or radians).

Why Use a Tangent Function Calculator?

  1. Trigonometric Problems – Essential for solving right triangle problems, particularly when you know the opposite and adjacent sides.
  2. Physics & Engineering – Used in problems involving angles of inclination, optics, and waves.
  3. Mathematics & Calculus – Appears in calculus, particularly in derivatives and integrals involving trigonometric functions.
  4. Real-world Applications – Used in surveying, architecture, and navigation, where precise angle measurements are important.

How Does It Work?

The calculator follows these steps:

  1. Take the input x (the angle in degrees or radians).
  2. Compute sin(x) and cos(x) (sine and cosine of the angle).
  3. Apply the formula: tan(x) = sin(x) / cos(x).
  4. Display the result.

Example:
If x = 45°,

  • sin(45°) ≈ 0.7071
  • cos(45°) ≈ 0.7071
  • tan(45°) = 0.7071 / 0.7071 = 1

If x = 90°,

  • tan(90°) is undefined (because cos(90°) = 0, division by zero).

When Do You Need a Tangent Function Calculator?

  • When solving right triangle problems, especially with the opposite and adjacent sides known.
  • In physics, when analyzing slopes, angles of inclination, and wave behavior.
  • For performing calculus involving trigonometric functions.
  • In real-world applications like navigation, construction, and land surveying.