Hyperbolic Tangent Function Calculator
What is a Hyperbolic Tangent Function Calculator?
A Hyperbolic Tangent (tanh) function calculator computes the tanh(x) of a given input x. The hyperbolic tangent is a hyperbolic function, and it's defined by the following formula:
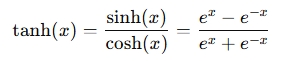
where e is the base of the natural logarithm (approximately 2.71828), and x is a real number input.
Why Use a Hyperbolic Tangent Function Calculator?
- Mathematics & Calculus – Hyperbolic functions, like tanh(x), appear in solving certain differential equations, particularly in hyperbolic geometry.
- Physics & Engineering – Used in wave equations, electric circuits, and phenomena involving exponential growth or decay.
- Computer Science – Applied in neural networks (activation functions) and algorithms for processing data in machine learning.
- Signal Processing – Useful in analyzing signals, filters, and systems with exponential growth or decay characteristics.
How Does It Work?
The calculator follows these steps:
- Take the input x (real number or angle).
- Compute e^x and e^(-x) (raise e to the power of x and its negative).
- Apply the formula:
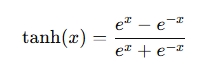
- Display the result.
Example:
If x = 1,
- tanh(1) = (e^1 - e^(-1)) / (e^1 + e^(-1)) ≈ 0.7616
If x = 0,
- tanh(0) = 0 (since e^0 = 1).
When Do You Need a Hyperbolic Tangent Function Calculator?
- When solving problems involving hyperbolic geometry or differential equations.
- In physics, particularly for systems with exponential behaviors like heat diffusion or wave propagation.
- In machine learning, particularly in training neural networks where tanh(x) is used as an activation function.
- In signal processing or communications, for analyzing systems with exponential growth or decay.