Arbitrary Triangle Calculator
Arbitrary Triangle Calculator
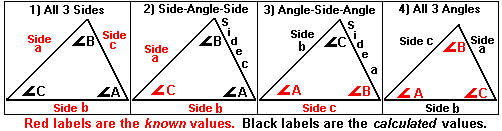
What is an Arbitrary Triangle Calculator?
An Arbitrary Triangle Calculator is a tool used to solve any type of triangle, whether it's a right triangle, an acute triangle, or an obtuse triangle. This calculator can determine missing sides, angles, and other properties of the triangle, regardless of whether it follows a specific rule (like being a right triangle). It applies various laws, such as the Law of Sines and Law of Cosines, to compute values based on the available information.
Why Use an Arbitrary Triangle Calculator?
- Solving any triangle: It works for all types of triangles (right, acute, obtuse), not just specific ones like right triangles.
- Convenient for complex problems: Helps to quickly solve triangles where you may only know a few sides or angles.
- Time-saving: Avoids the lengthy process of manually applying trigonometric formulas and theorems.
- Accurate results: It reduces the risk of errors that can occur in manual calculations.
How Does an Arbitrary Triangle Calculator Work?
- Input known values:
- Three sides (SSS): If you know all three sides, the calculator uses the Law of Cosines to find the angles.
- Two sides and the included angle (SAS): If you know two sides and the angle between them, the calculator uses the Law of Cosines to find the third side and angles.
- Two angles and one side (AAS or ASA): If you know two angles and one side, the calculator uses the Law of Sines to find the other angles and sides.
- One side and two angles (SSA): If you know one side and two angles, it uses the Law of Sines to calculate the missing side and angles.
- Apply the relevant laws:
- Law of Sines:
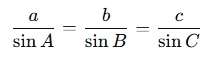
- Law of Cosines:
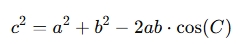
- Law of Sines:
- Calculate the missing values (side lengths, angles) and display the result.
When to Use an Arbitrary Triangle Calculator?
- When solving triangles with unknown angles or sides: For non-right triangles, such as when you have SSA, AAS, or SAS information.
- In geometry: When working with polygons, trigonometry, or calculating areas and angles of arbitrary triangles.
- In physics and engineering: For resolving forces, vectors, and other applications involving non-right triangles.
- In surveying and navigation: For calculating distances and angles in fields like mapping or land surveying.
- In real-world problem solving: When determining dimensions and angles of irregular shapes, such as in architecture, construction, or astronomy.