X and Y Intercept Calculator

An X and Y Intercept Calculator is a tool used to calculate the intercepts of a linear equation or function on a graph. Specifically, the X-intercept is where the graph crosses the X-axis (where y = 0), and the Y-intercept is where the graph crosses the Y-axis (where x = 0).

Why use an X and Y Intercept Calculator?

• Quickly find intercepts: It simplifies the process of finding where a line or curve intersects the axes, which is useful for graphing and analyzing linear functions.
• Understanding graph behavior: The intercepts provide critical information about the position and behavior of the graph, especially for linear equations.
• Solving equations: It helps solve problems where you need to quickly identify the points of intersection with the axes, which can be part of larger algebraic or geometric problems.

How does an X and Y Intercept Calculator work?

For a linear equation in the form:

where:

• mm m is the slope of the line.
• b is the Y-intercept (the value where the line crosses the Y-axis).

To find the intercepts:

1. Y-intercept:

   • Set x = 0 in the equation and solve for y: y = m(0) + b = b
   • So, the Y-intercept is simply b (the constant term in the equation).

2. X-intercept:

   • Set y=0 in the equation and solve for x:
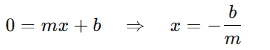
   • So, the X-intercept is ​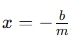 , which is the point where the line crosses the X-axis.

When to use an X and Y Intercept Calculator?

• Graphing linear equations: Whenever you are graphing a line and need to quickly find where it intersects the axes.
• Solving problems in algebra: In problems involving linear equations, finding the intercepts is often a key step in solving the problem.
• Analyzing real-world situations: In areas like economics, physics, and engineering, intercepts can represent important values such as starting points (Y-intercept) or break-even points (X-intercept).
• Checking solutions: In some cases, the intercepts can provide an easy way to check the correctness of a given equation or solution.

Example:

For the equation y = 2x + 4:

• Y-intercept: Set x=0, so y=2(0)+4=4. The Y-intercept is (0,4).
• X-intercept: Set y=0, so 0=2x+4. Solving for x, we get x=−2. The X-intercept is (−2,0).