Two point Slope form calculator - Find equation of a straight line

Enter value and click on calculate. Result will be displayed.
x1:
x2:
y1:
y2:
Result:

What is the Two-Point Slope Form of a Line?

The Two-Point Slope Form is a way to express the equation of a straight line using the coordinates of two points that lie on the line. The formula is:

y−y1=m(x−x1)

Where:

  • (x1,y1)are the coordinates of the first point.

  • mm m is the slope of the line, calculated as the change in y divided by the change in x, or the "rise" over "run":

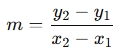
  • (x2,y2)are the coordinates of the second point.

Why Use the Two-Point Slope Form?

The two-point slope form is useful when you know the coordinates of two points on the line, but not the slope or the y-intercept. It's a quick way to find the equation of a line without needing to convert to slope-intercept form (y = mx + b), especially when the two points are already known.

How Does It Work?

  1. Calculate the slope (m) of the line using the formula:
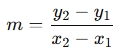
  2. Substitute the slope into the two-point slope equation.
  3. Substitute the coordinates of one of the points (either (x1,y1)or (x2,y2)) into the equation.

This will give you the equation of the line that passes through the two points.

When to Use the Two-Point Slope Form?

You would use the two-point slope form when you know:

  • Two points that the line passes through.
  • The need to quickly determine the equation of the line.

It is often used in geometry, algebra, and physics when working with coordinate systems and straight-line relationships between variables.

Example:

Given two points: (1,2)and (3,6)

  1. Calculate the slope:

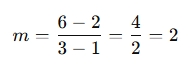
  2. Substitute m=2 and one of the points, say (1,2), into the two-point slope formula:

    y−2=2(x−1)

  3. Simplify the equation:

    y−2=2x−2
    y = 2x

So, the equation of the line passing through (1,2)and (3,6) is y=2x.