Angular Acceleration Calculator

Enter value and click on calculate. Result will be displayed.

Formula:
α = 𝜏/I

Method :
 
Total torque :
rad/sec
Mass moment of inertia :
sec
Result:

An Angular Acceleration Calculator is a tool used to calculate the angular acceleration of an object rotating about an axis. Angular acceleration is the rate at which the angular velocity of an object changes over time.

Why use an Angular Acceleration Calculator?

  • Determine rotational dynamics: Angular acceleration is essential in understanding how fast an object is speeding up or slowing down as it rotates. This is important in mechanical systems, motors, wheels, and anything involving rotational motion.
  • Design and analysis: Engineers use angular acceleration to design rotating machinery and components (e.g., turbines, gears, engines), ensuring they operate efficiently and within safe limits.
  • Simplify calculations: It simplifies the process of calculating rotational motion parameters without the need for manual, complex computations.

How does an Angular Acceleration Calculator work?

  • Formula: Angular acceleration α\alpha α is calculated using the following basic equation:

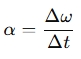
    where:

    • α is the angular acceleration (in radians per second squared, rad/s2).
    • Δω is the change in angular velocity (in radians per second).
    • Δt is the time taken for the change in velocity (in seconds).

    In other cases, if the object is subject to a torque (τ), angular acceleration is related to the moment of inertia (I) of the object by the equation:

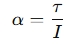
    where:

    • τ is the torque applied (in Newton-meters, N⋅m).
    • I is the moment of inertia of the object (in kg⋅m2).

  • Using the calculator: You can input values like initial and final angular velocity, time interval, torque, or moment of inertia, and the calculator will compute the angular acceleration for you.

When to use an Angular Acceleration Calculator?

  • Rotational motion problems: Whenever you're dealing with objects in rotational motion and need to find out how quickly their angular velocity is changing.
  • In mechanical engineering: For designing rotating parts (like wheels, gears, motors), where you need to know how fast a component accelerates or decelerates.
  • In physics: In understanding the dynamics of rotating systems, like planets, satellites, or mechanical devices.
  • For control systems: When designing control systems for motors and robots, angular acceleration helps determine how quickly a system can respond or change speeds.