P(X = r) = nCr pr (1-p)(n-r)
Binomial Distribution Calculator
What is a Binomial Distribution Calculator?
A Binomial Distribution Calculator is a tool that computes probabilities for binomial distributions, which model situations where there are two possible outcomes (success or failure) in a fixed number of independent trials. The binomial distribution is commonly used in statistics to model events like flipping a coin, passing a test, or quality control in manufacturing.
The binomial probability formula is:
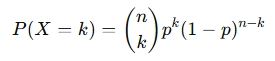
Where:
- P(X=k)= Probability of exactly kk k successes
- n = Number of trials
- k = Number of successes
- p = Probability of success on a single trial
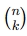 = Binomial coefficient, or "n choose k"
= Binomial coefficient, or "n choose k"
Why use a Binomial Distribution Calculator?
- Statistical Analysis: It simplifies the process of calculating probabilities for binomial events, which is useful in various fields like quality control, health studies, and economics.
- Hypothesis Testing: In statistical testing, the binomial distribution is often used for hypothesis testing, such as determining whether a process is operating at expected levels.
- Decision-Making: Helps businesses and researchers make informed decisions based on probabilistic models of success/failure scenarios.
How does a Binomial Distribution Calculator work?
- Input: You provide the number of trials nn n, the probability of success pp p, and the number of successes k.
- Process: The calculator applies the binomial probability formula to compute the probability of observing exactly k successes in n trials.
- Output: The result is the probability value P(X=k), which tells you the likelihood of observing kk k successes in the given trials.
For example, if you flip a coin 5 times (n=5), and the probability of getting heads (success) on each flip is 0.5 (p=0.5), the probability of getting exactly 3 heads (k=3) is:
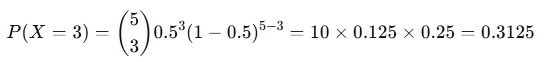
When should you use a Binomial Distribution Calculator?
- Quality Control: In manufacturing or quality control, to calculate the probability of a certain number of defective items in a batch of products.
- Clinical Trials: To model the probability of a certain number of successes (such as patients showing improvement) in clinical trials.
- Polls and Surveys: When calculating the probability of a certain number of "yes" responses or favorable outcomes in surveys or polls.
- Games of Chance: For problems like rolling dice, flipping coins, or drawing cards, where there are fixed trials and two possible outcomes.