Complex Number Calculator

Enter value and click on calculate. Result will be displayed.

Formula:
Addition = (a+bi) + (a+bi)

Select calculator :
 
a :
bi :
a:
bi:
Result:
---
---

What is a Complex Number Calculator?

A Complex Number Calculator is a tool that helps perform operations (such as addition, subtraction, multiplication, division, and finding magnitudes) on complex numbers. Complex numbers are numbers that have a real part and an imaginary part, usually written as:

z=a+bi

Where:

  • a is the real part,
  • b is the imaginary part,
  • i is the imaginary unit (i2=−1).

Why use a Complex Number Calculator?

  • Mathematical Applications: Complex numbers are widely used in mathematics, physics, and engineering for solving equations that don’t have real solutions.
  • Ease of Calculation: Complex numbers can be tricky to handle manually, especially for operations like multiplication, division, and finding roots.
  • Advanced Functions: Helps compute advanced functions like powers, logarithms, or exponentials of complex numbers.

How does a Complex Number Calculator work?

  1. Input: Enter two complex numbers, often in the form a+bi or r(cos θ + i sin θ) (polar form).
  2. Operations: Choose the desired operation, such as addition, multiplication, modulus (magnitude), or argument.
  3. Output: The calculator will provide the result in either rectangular form (a+bi) or polar form (reiθ).

For example:

  • Addition: (3+2i)+(1+4i)=4+6i
  • Modulus: The modulus of

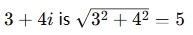
When should you use a Complex Number Calculator?

  • Solving equations: When solving quadratic equations with no real solutions or working with polynomials.
  • Electrical Engineering: Complex numbers are used for analyzing AC circuits and signal processing.
  • Physics: In quantum mechanics, fluid dynamics, and other areas where complex numbers are essential.
  • Signal Analysis: Complex numbers simplify the representation of signals in the frequency domain.