Cone Calculator

Enter value and click on calculate. Result will be displayed.

Formula:
Volume = (1/3) πr2h

Radius (r) :
Height (h) :
Result:
Slant Height(l) of Cone [ Sqrt(r² + h²) ] :
Volume of Cone [ (1/3)πr²h ] :
Curved Surface Area(CSA) of Cone [ πrl ] :
Total Surface Area(TSA) of Cone [ πr(l+r) ] :

What is a Cone Calculator?
A cone calculator is a tool that helps you quickly determine key measurements of a cone — a three-dimensional shape with a circular base that tapers smoothly to a single point (apex). Using basic inputs like the cone’s radius, height, or slant height, the calculator can compute:

  • Volume: The amount of space inside the cone
  • Surface Area: The total area of the cone’s curved surface and base
  • Slant Height: The distance from the base’s edge to the apex along the cone’s surface
  • Base Area: The circular base’s area
  • Lateral Surface Area: The curved surface area only

Why use a Cone Calculator?

  • Saves time: Quickly calculates complex cone measurements
  • Reduces error: Avoids mistakes in manual calculations
  • Practical use: Helps in design, manufacturing, and construction
  • Educational tool: Aids in learning 3D geometry concepts

How does a Cone Calculator work?
Using known formulas, a cone calculator works based on two primary inputs — the cone’s radius (r) and height (h). From there, it computes:

  1. Slant height (s): The distance from the base’s edge to the apex

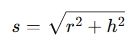
  2. Volume (V): The amount of space the cone encloses

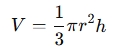
  3. Base area (A_b): The circular base’s surface area

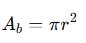
  4. Lateral surface area (A_l): The curved surface area

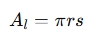
  5. Total surface area (A_t): The entire outer surface of the cone (base + lateral)

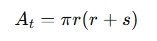
Example Calculation:
For a cone with:

  • Radius r = 5 units
  • Height h = 12 units

  1. Slant height:

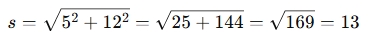
  2. Volume:

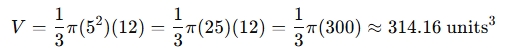
  3. Base area:

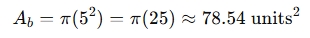
  4. Lateral surface area:

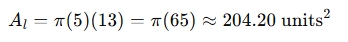
  5. Total surface area:

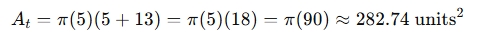
When is a Cone Calculator used?

  • Construction: Calculating concrete volumes for cone-shaped structures
  • Manufacturing: Designing objects like funnels or conical containers
  • Art and design: Creating cone-based sculptures or decorations
  • Education: Solving geometry problems involving 3D shapes
  • Physics and engineering: Calculating airflow, pressure distribution, or fluid volume in conical tanks