Cubic Equation Solver
What is a Cubic Equation Solver?
A cubic equation solver is a tool or program designed to find the roots (solutions) of a cubic equation — an equation where the highest power of the variable is three. A standard cubic equation looks like:
Where:
- a, b, c, and d are real numbers (coefficients)
- a≠0 (otherwise it wouldn’t be a cubic equation)
- x represents the unknown variable
The roots of the equation are the values of x that satisfy the equation. A cubic equation can have:
- One real root and two complex roots
- Three distinct real roots
- Multiple real roots with multiplicity
Why use a Cubic Equation Solver?
- Accuracy: Solving cubic equations by hand can be complicated and prone to mistakes.
- Efficiency: It saves time, especially when working with difficult or large coefficients.
- Complex numbers: It easily handles cases where roots include imaginary numbers.
- Applications: Used in physics, engineering, economics, and computer science for modeling real-world problems.
How does a Cubic Equation Solver work?
A cubic solver typically follows these steps:
- Input the coefficients: a, b, c, and d.
- Discriminant calculation: Determines the nature of the roots (real or complex).
- Find the roots: Uses mathematical formulas or numerical methods to solve for x:
- Cardano’s formula: An algebraic solution for cubic equations.
- Numerical methods: Like Newton-Raphson or synthetic division for approximations.
- Output the roots: Displays the real and/or complex roots of the equation.
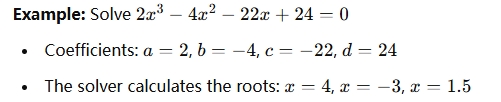
When is a Cubic Equation Solver used?
- Engineering: Calculating structural loads and forces.
- Physics: Solving equations of motion, fluid dynamics, and energy transfer.
- Economics: Modeling supply and demand curves, profit maximization.
- Computer graphics: Working with curves and 3D modeling.
- Algebra and calculus: Factoring polynomials and finding critical points.